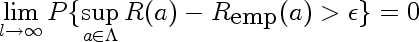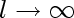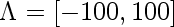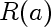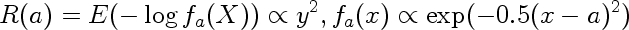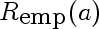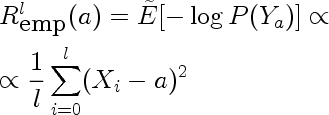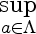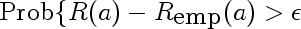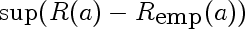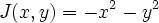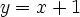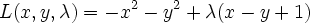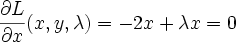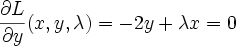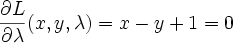You can see there's a blip at 1983 when the workshop was held.
Yann LeCun quipped at NIPS closing banquet that people who joined the field in the last 5 years probably never heard of the word "Neural Network". Similar search (normalized by results for "machine learning") reveals a recent downward trend.
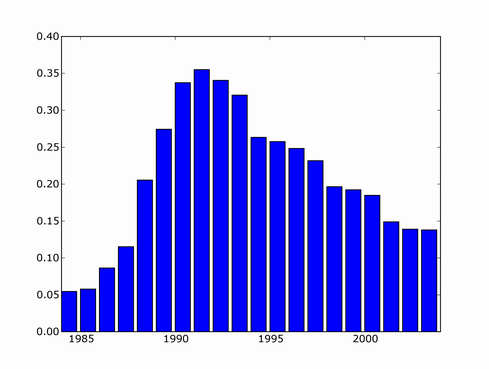
You can see a major upward trend starting around 1985 (that's when Yann LeCun and several others independently rediscovered backpropagation algorithm), peaking in 1992, and going downwards from then.
An even greater downward trend is seen when searching for "Expert System",

"Genetic algorithms" seem to have taken off in the 90's, and leveled off somewhat in recent years

On other hand, search for "support vector machine" shows no sign of slowing down

(1995 is when Vapnik and Cortez proposed the algorithm)
Also, "Naive Bayes" seems to be growing without bound

If I were to trust this, I would say that Naive Bayes research the hottest machine learning area right now
"HMM"'s seem to have been losing in share since 1981

(or perhaps people are becoming less likely to write things like "hmm, this result was unexpected"?)
What was the catastrophic even of 1981 that forced such a rapid extinction of HMM's (or hmm's) in scientific literature?
Finally a worrying trend is seen in the search for "artificial stupidity" divided by corresponding hits for "artificial intelligence". The 2000 through 2004 graph shows a definite updward direction.