The important equation is the following:
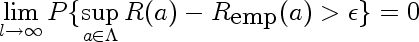
Here I'll explain the parts of the formula using the following motivating example:
Suppose our true distribution is a normal distribution with unit variance, centered at 0, and we estimate its mean from data using method of maximum likelihood. This falls into domain of Empirical Risk Minimization because it's equivalent to finding unit variance normal distribution which minimizes empirical log-loss. If this method is consistent, then our maximum likelihood estimate of the mean will be correct in the limit
In order for the theorem to apply, we need to do make sure that we can put a bound on the loss incurred by functions in our hypothesis space, so here, make an additional restriction that our fitted normals must have mean between -100 and 100.
Here's what parts of the equation stand for
1.
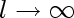
l is the size of our training set
2.
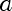
a is the parameter that indexes our probability distributions, in this case, it's mean of our fitted Normal. Lambda is it's domain, in this case,
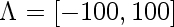
3.
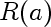
This is the actual risk incurred by using estimate a instead of true estimate (0). In our case the loss is log loss, so the risk is
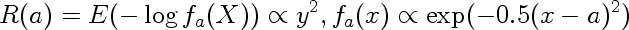
In other words it is the expected value of the negative logarithm of the probability assigned to observations when observations come from Normal centered at 0, but we think they come from Normal centered on a
4.
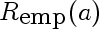
This is the risk incurred by using estimate a, estimated on a finite sample drawn from the true density. In our case it is the following
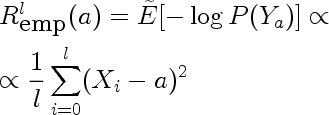
Because the sample is a random variable, empirical risk is also a random variable. We can use the method of transformations to find it's distribution. Here are distributions for empirical risk estimated from training sets of size one for different values of a.

You can see that the modes of the distributions correspond to the true risk (a^2), but the means don't.
5.
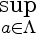
Supremum is defined as the least upper bound, and behaves lot like maximum. It is more general than the maximum however. Consider the sequence 0.9, 0.99, 0.999, ....
This sequence does not have a maximum but has a supremum.
6.
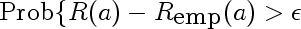
This is the simplified middle part of the equation. It represents the probability of our empirical risk underestimating true risk by more than epsilon, for a given value of a. This would be used in place of the supremum if we cared about pointwise as opposed to uniform, convergence. Intuitively, we expect this probability to get smaller for any fixed epsilon as the sample size l gets larger. Here are a few densities of risk distribution for a=4 and different values of l

7.
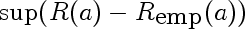
This is the random variable that represents the largest deviation of the empirical risk from corresponding true risk, over all models a. It's like an order statistic, except the samples are not IID, and there are infinitely many of them.
Questions:
- How can one find the distribution of \sup(R(a)-R_emp(a) in the setting above?
13 comments:
Hi Yaroslav.
I'm learning Bayesian nets in CS 430 -- it's fun. I just wanted to say "hi" on your blog. Hope you're having fun in school.
P.S.: If you haven't seen it yet, the Banach fixed point theorem gives a nice test for convergence of iterated functions.
Some of people do the post aicm now and they do it before usmle. It is really surprising that they choose this first and it could be tough at beginning but they can easily get it later. nice article & it will give you some amazing idea and very effective for the papers writing.
While I was going to learn some theory it really gives me pain as ther ehas hardship but here are some tips which help me out. website you'll be find some helpful information about the academic writing service.
There has nothing special you can do in the theory side if you do not study and try to practice it in your own way at home. look here for the students that is very helpful for the writing services.
My best friend send me the link and told me that you go to the page and visit there. Because this page share their post for the people like you. That's why I'm here. SO good really. Thanks to my friend for this link.
I am weak in The Key Theorem of the Learning Theory but I am very well with graf. I see you posted both of information here. its impresed me. I will check more info from your website in future. thanks
Excellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
Nice one, I guess we just need to stop for a brief moment and read through. I dont read that much but I really had some good time grabbing some knowledge. Still I am out to speak and propose you exotic stuffs like
exotic carts official
buy exotic carts
buy exotic carts online.
exotic carts review
exotic carts website
gorilla glue exotic carts.
exotic carts fake
kingpen official
kingpen review.
mario carts official
mario carts online
exotic carts website
exoticcartsofficial
exotic carts for sale
exotic carts thc
exotic cartridges
exotic carts flavors
@exoticcartsofficial
real exotic carts
exotic carts vape cartridges
exotic cart
exotic carts vape pen
mario kart cartridge
king pen battery
exoticcarts
exotic carts official website
supreme cartridges
mario carts cartridges
exotic carts review
710 kingpen gelato
710 king pen battery
supreme cartridge
supreme brand oil cartridge
what are exotic carts
what are pre roll
what are dabwoods
In each dialogue box, the movies chronologically segregated in descending order.
This site is very organized and very possible. The film can be searched alphabetically.
From 0-9 and the alphabets individually can be searched.Hollywood, Bollywood, Malayalam, Tamil
and Telugu movies. Once you open the website, you will be able to see a range of options.123Movies,
GoMovies, GoStream, MeMovies or 123movieshub,movierulz,hindi movies,Bollywood | Hollywood | Songs | Punjabi
| Hindi Dubbed | Songs | Hindi Webseries Season | Netfilix | ULLU App
In a separate dialogue box, we can search by the plethora of the genres provided to us. Action, animation, adventure,
biography, comedy, crime, documentary, drama, family, fantasy, film-noir, game show, history, horror, music, musical, mystery,
news, reality show, romance, sci-fi, sports, talk- show, thriller, war and western and various genres can be found here.
Any web site offered u . s . by means of vital info for work relating to. ดูการ์ตูน
https://dramasnite.net/
check out my websites
dramasnite
hum tv dramas
ary digital dramas
Geo tv dramas
Dil Zar Zar
Badzaat
check out my articles
https://zarasocial.com/
zarasocial
actor
actress
Your blogs are really good and interesting. I came across an interesting article by Zhu and Lu talking about how non-informative priors can often be counter-intuitive. For instance suppose we are estimating parameter of a Bernoulli distribution. It is very great and informative Fairfax Traffic Lawyer. I got a lots of useful information in your blog. Keeps sharing more useful blogs..
Post a Comment