You have to enter resistance between A and B in the diagram below. Can you do it?
Wednesday, December 26, 2007
Russian CAPTCHA
Here's an innovative CAPTCHA I came across when trying to register for a forum at http://lib.mipt.ru/?spage=reg_user
You have to enter resistance between A and B in the diagram below. Can you do it?
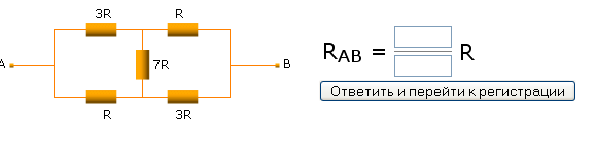
You have to enter resistance between A and B in the diagram below. Can you do it?
Monday, December 17, 2007
Sampling doubly stochastic matrices
Stochastic matrices are easy to get -- just normalize the rows. Doubly stochastic matrices require more work -- simply normalizing columns/rows will not converge may take few dozen iterations to converge. One approach that works is to do constrained optimization, finding closest (in least squared sense) doubly stochastic matrix to given matrix. Another approach is to start with a permutation matrix and follow a Markov chain that modifies 4 elements randomly at each step in a way that keeps the matrix doubly stochastic. Here is the implementation of these two methods in Mathematica (notebook in the same directory)
http://www.yaroslavvb.com/research/qr/doubly-stochastic/doubly-stochastic.html
As Jeremy pointed out, Birkhoff's theorem provides necessary and sufficient conditions for a matrix to be doubly stochastic -- it must be a convex combination of permutation matrices. It seems hard to sample from the set of valid convex combinations though. For instance, here's a set of 3 dimensional slices through the set of valid convex combinations for 3x3 matrices (there are 6 permutation matrices, so the space is 5 dimensional).

Update: here's the updated notebook with 2 more algorithms, suggested by Dr.Teh and Jeremy below. Turns out that sampling random convex combinations is fairly easy -- almost all the time uniformly sampled convex combination will produce a doubly-stochastic matrix. However, matrices end up looking pretty uniform
http://www.yaroslavvb.com/research/qr/doubly-stochastic/doubly-stochastic3.html
http://www.yaroslavvb.com/research/qr/doubly-stochastic/doubly-stochastic.html
As Jeremy pointed out, Birkhoff's theorem provides necessary and sufficient conditions for a matrix to be doubly stochastic -- it must be a convex combination of permutation matrices. It seems hard to sample from the set of valid convex combinations though. For instance, here's a set of 3 dimensional slices through the set of valid convex combinations for 3x3 matrices (there are 6 permutation matrices, so the space is 5 dimensional).

Update: here's the updated notebook with 2 more algorithms, suggested by Dr.Teh and Jeremy below. Turns out that sampling random convex combinations is fairly easy -- almost all the time uniformly sampled convex combination will produce a doubly-stochastic matrix. However, matrices end up looking pretty uniform
http://www.yaroslavvb.com/research/qr/doubly-stochastic/doubly-stochastic3.html
Subscribe to:
Posts (Atom)