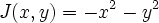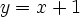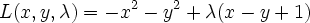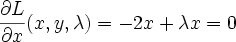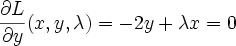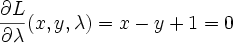Blogs of Note

From Geomblog -- "Machine learning blogs appear to be popping up faster than you can say 'expectation-maximization'". With that note, here are a few machine learning (and related) blogs I came across recently

Technical

• Machine Learning -- Eric Altendorf is a grad student doing research on Knowledge Intensive learning here at OSU
• Machine Learning -- Josek is a PhD student working on Bayesian Learning
• Alpha and Beta -- (two stats grad students?)

Non-Technical

• BMI students -- a group of students in a graduate BioInformatics program
• Math4Poets -- math history
• Treadmill to Infinity -- AI researcher at MIT
• Sam Reid's blog -- grad student at U.Colorado, does Machine Learning research
  Yin Zhangqi's Blog -- physics grad student. It's mostly in Chinese, but with google's translator, and good deal of imagination, you can read some things

Knowledge Intensive Learning

When prior knowledge is given in the form of a prior, Bayesian method is the rational way of making decisions, based on Cox' arguments. However, prior knowledge doesn't usually come in a form of a prior. For instance an expert may say that X and Y are independent, or that increasing value of X will influence Y to increase. We need to figure out how to use those kinds of knowledge to bias our learners, and this is where Knowledge Intensive Learning comes in. Eric Altendorf does research in the area and is doing a series of posts on it in his new blog.

Naive Bayes to fight HIV?

Quoting -- "Microsoft scientists David Heckerman and Nebojsa Jojic were the first to pioneer the medical uses of anti-spam software. They have joined up with doctors and scientists from the University of Washington and Australia's Royal Perth Hospital to build more potent vaccines based on the data gathered by Microsoft's technologies."

article

How to browse the web while pretending to do Machine Learning research

• Browse ML-related tags on Del.icio.us (http://del.icio.us/tag/machinelearning)
• Find people who bookmarked JMLR and browse their bookmarks/inbox (ie http://del.icio.us/dnaboy76)
• Search for "Machine Learning" on technoratid (search)
• Find people who subscribed to John Langford's blog through bloglines, and browse their subscriptions, (ie http://bloglines.com/public/Suresh)
• Find people who entered ML papers in Citeulike, and browse their library (ie http://www.citeulike.org/user/brian)
• At some point, get back to work ;)

Questions:

• What are some other ways of finding interesting stuff?

CiteULike

I came across CiteULike on Seb's Open Research blog a week ago, tried it out, and it seems very useful. Basically it's a cross between bibliography management software like JafRef, and social bookmarking like del.icio.us. You can use it to keep track of the papers you find, and export in the BibTex format. Then you can see what other people added given paper, and see what papers they are reading. You can also add comments to papers and view other people's comments (not many at this point). Suresh has a more detailed review.

Resources:

• http://www.citeulike.org/
• CiteULike FAQ
• Papers I've added to it recently
  

Machine Learning reading groups

If you are looking for ideas for things to read, you should check out what other Machine Learning Reading Groups are reading. I compiled the following list by searching google/asking people.

This list is not very up to date. This is a permalink so feel free to link to it. Please let me know through email, or comment section about other up-to-date MLRGs you know (site must list papers)

Current MLRGs
(as of Feb 19th 2005)

• Oregon State U (Roweis, Tishby, Jordan, Collins, Caticha)-- mlrg
  
• Gatsby (McKay, ARD, LDA) -- mlrg
  
• Humboldt-Universitat zu Berlin (ICML, KDD papers)-- mlrg
  
• TTIC Chicago list of readings (Langford, Kakade, McAllester)seminars
  
• University of New Mexico (Jaakkola, Mooney, Scholkopf) -- mlrg
  
• Oregon Health and Science U. (Seeger, Geman, MacKay) -- mlrg
  
• Washington University (Weiss, Srebro) -- mlrg
  
• MIT (Neal, Hofmann, Tishby) -- mlrg
  
• University of California, Irvine (Blei, Jordan, Welling) -- mlrg
  
• University of Amsterdam (Manning, Koller, Collins, Valiant) mlrg
  
• Hebrew University (IB, SVM, Rademacher, Chechnik) mlrg
  
• Cornell (Jordan, Schuurmans,Cristianini) -- mlrg
  
• South Carolina (Kakade, Dresner, Feigenbaum) mlrg
  
• U. Alberta (Sutton, RL, MaxEnt)-- mlrg
  
• Weizemann Institute, (vision oriented, Jordan, Buntine) -- mlrg
  
• Helsinki U of Tech (mostly neuroscience, Sejnowski) -- mlrg
  
• University of London (vision oriented) -- mlrg
  
• Rutgers (Michael Jordan's notes) -- mlrg
  
• UMass (vision oriented, ICA, kernel PCA) -- mlrg
  
• Edinburgh (NLP group, Hoffman, Manning,Collins) -- mlrg
  
• U. of California, San Diego (Tishby, Lafferty, Joachims, Herbrich) -- mlrg
  
• UTexas (Aggarwal, Altun, Manning) -- mlrg
  

Seminars,Journal Clubs,slightly outdated MLRGs

• Columbia (November) -- mlrg
  
• U.Toronto (July)-- mlrg
  
• Tufts University (December) -- mlrg
  
• Australian National U. (December)-- mlrg
  
• Centre Universitaire d'Informatique (June) --journal club
  
• Microsoft Research (Herbrich, large-margin, factor graphs, kernels) -- mlrg
  
• CWI Journal Club (Netherlands) journal club
  
• Seminars at NYU (Langford, Saul) seminars
  
• Graphical Models Reading Group at CMU (about 10 months old) mlrg
  

Who is being read?
Below is the list of most popular authors ranked by how many groups in the "current MLRGs" section had them listed:

9 - Koller
8 - Jordan
7 - Weiss
6 - Taskar, Saul, McCallum, Lafferty, Ghahramani, Friedman, Collins
5 - Roweis, Pereira, Ng, Domingos
4 - Zhu, Tishby, Russell, Roth, Li, Kearns, Jaakkola, Guestrin, Blei
3 - Zhou, Yair, Wong, Wellner, Tenenbaum, Slonim, Singh, Singer, Scholkopf, Schapire, Mooney, Mansour, Manning, MacKay, Joachims, Hofmann, Griffiths, Freund, Freeman, Dengyong, Breiman, Bartlett, Altun

Questions:

• What other reading groups have websites?
• What are other ways of finding interesting papers?

Category: MachineLearning

Tensor Methods for Optimization

Second-order methods use an exact Hessian, or a compact approximation to direct the search for the minimum. They are called second-order because the Hessian they use, ie, second derivative, is the second order term in the Taylor expansion of the function. What if our function is not a quadratic, and we wanted to guide our minimization using some 3rd or 4th order information? That's where tensor methods come in.


Description

Main idea to Schnabel's tensor method is to select a set of p points from previous evaluations such that they are mostly linearly independent (each new direction makes at least a 45 degree angle with old direction). The idea is then to try to interpolate function values at those points by fitting a 4th order model with special form of 3rd and 4th order terms. Because of the restricted form of these terms, the overhead associated with this step is not significant over the standard Newton-Gauss algorithm. Because it approximates function with 4th order expansion, the number of problems for which this method converges was larger. Schnabel also proves superlinear convergence of this method for some cases when Newton's method converges linearly.

Performance

Seth Greenblatt tried tensor method on some econometric models, and results were 1.5-3 times reduction in number of function evaluations. He compared it against Newton-Rhapson method, using exact matrix inversion (O(n^3)) and the extra overhead of for the tensor method wasn't significant. The problems he tested on were econometric models including Lucas-Rapping model and Berndt-Wood KLEM model. Lucas-Rapping model in his thesis was basically logistic regression with some econometric semantics.

Schnabel's paper in SIAM J Opt also used explicit Hessian, and O(n^3) steps to invert it. His 1998 paper introduces implementation of tensor method, TenSolve, which uses same approach as Gauss-Newton to approximate second order term from gradients, which means O(n^2) space and time requirement. Asymptotic overhead of using tensors was O(n^1.5)

Thoughts

TenSolve stores the approximation to the Hessian explicitly, so that takes O(n^2) space. It seems conceptually possible to reduce storage to O(n) if we use a method analogous to limited memory BFGS to store the Hessian. If that worked, it would result in a tensor optimization method with O(n) storage complexity and O(n^1.5) computation complexity

• What are some applications of Machine Learning where an O(n^1.5) method would be acceptable?
• What would be a good dataset on which to test CRF training using this method?

Resources:

• Schnabel, Robert B and Ta-Tung Chow (1991) "Tensor Methods for Unconstrained Optimization Using Second Derivatives," SAIM J. Optimization 1,3,293-315
• Ali Bouaricha, Robert B. Schnabel: Algorithm 768: TENSOLVE: A Software Package for Solving Systems of Nonlinear Equations and Nonlinear Least-Squares Problems Using Tensor Methods. ACM Trans. Math. Softw. 23 (2): 174-195 (1997)
• Greenblatt, "Tensor Methods for Full-Information Maximum Likelihood Estimation", PhD thesis, George Washington University
• TenSolve (Implementation of Schnabel's tensor optimization method): http://www.netlib.org/toms/768

Uninformative Priors

I came across an interesting article by Zhu and Lu talking about how non-informative priors can often be counter-intuitive. For instance suppose we are estimating parameter of a Bernoulli distribution. If we don't know anything, the most intuitive prior to use is uniform. However Jeffreys' "uninformative" prior doesn't look uniform at all:



This prior seems to favour values of theta close to 0 or 1, so how can it be uninformative?


The intuition they provide is the following: think of Maximum Likelihood estimator as the most uninformative estimate of parameters. Then we can rank informativeness of priors by how closely the Bayesian Posterior Mean estimate comes to the maximum likelihood estimate.

If we observed k heads out of n tosses, we get following estimates:

1. MLE: k/n
2. PM using Jeffrey's prior (k+1/2)/(n+1)
3. Laplace smoothing (Uniform) (k+1)/(n+2)
4. PM using Beta(a,b) prior (k+a)/(n+a+b)

You can see that using this informal criteria for informativeness, Jeffreys' prior is more uninformative than Uniform, and Beta(0,0) (the limiting distribution) is the least informative of all, because then Posterior Mean estimate will coincide with the MLE.

Resources:

• Zhu, Lu, The Counter-intuitive Non-informative Prior for the Bernoulli Family, Journal of Statistics Education Volume 12, Number 2 (2004), http://www.amstat.org/publications/jse/v12n2/zhu.pdf
• Kass, Wasserman, "The Selection of Prior Distributions by Formal Rules", JASA 96
• Anne Randi Syversveen. "Noninformative Bayesian priors. Interpretation and problems with construction and applications" (1998), unpublished http://www.math.ntnu.no/preprint/statistics/1998/S3-1998.ps

Why I started this blog

I've been doing research in Machine Learning (Conditional Random Fields and related) for the last year. This is a place for me to organize my thoughts and write down interesting new things I come across (but feel free to add comments). Some of the things I may be adding:

1. Comments on papers
2. Mini-tutorials on ML-related topics
3. Links to online Machine Learning resources

It won't be linear in nature as I'll revise old posts when relevant information comes up. Maybe in the future I'll switch to a setup similar to Cosma Shalizi's notebooks, but at this point, blog is the most practical thing to do.

Resources:

• Cosma Shalizi's notebooks http://www.cscs.umich.edu/~crshalizi/notebooks/

Lagrange multipliers: equality constraints

Constrained optimization often comes up in machine learning.

1. Finding lengths of best instantaneous code when distribution of source is known
2. Finding maximum entropy distribution subject to given constraints
3. Minimizing distortion specified by the amount of information X provides about Y (Tishby's, Information Bottleneck method)

All of the examples above can be solved using the method of Lagrange multipliers. To understand motivation for Lagrange multipliers with equality constraints, you should check out Dan Klein's excellent tutorial.

However, you don't have to understand them to be able to go through the math. Here's how you can do it in 5 easy steps:

Write down the thing you are optimizing as J(x)

1. Write down your constraints as g_i(x)=0
2. Define L(x,l1,l2,...)=J(x) + l1 g1(x) + l2 g2(x) +...
3. Differentiate L with respect to each variable and set to 0
4. Solve this system of equations

Small Example

Suppose you want to maximize


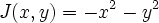
subject to

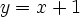
Your problem looks like this:

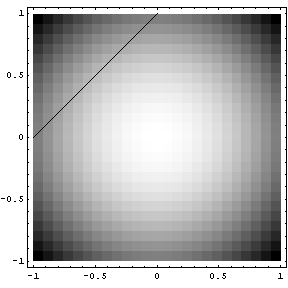
(black line is where you solution must lie)

Then our only constraint function is g(x,y)=x-y+1=0. Our L (Langrangian) then becomes

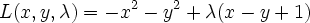
differentiating and setting to 0 we get

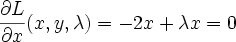
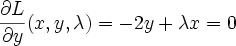
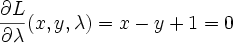
Solve this system of 3 equations by substitution and you get x=-0.5, y=0.5, lambda=-1. The lagrange multiplier lambda_i represents ratio of the gradients of objective function J and i'th constraint function g_i at the solution point (that makes sense because they point in the same direction)

Bigger Example

For a more realistic example, consider maximizing entropy over a set of discrete distributions over positive integers where the first moment is fixed. Since we have an infinite number of possible X's, differentiating the Lagrangian gives us an countably infinite system of equations. But that's not actually a problem (unless you try to write them all down). Here's the detailed derivation

http://yaroslavvb.com/research/reports/fuzzy/fuzzy_lagrange.ps

So you can see that highest entropy discrete distribution with fixed mean is geometric distribution. We can solve the same problem for continuous X's in the positive domain, and get exponential distribution. If we allow X's to span whole reals, there will be no solution for the same reason as why "uniform distribution over all reals" doesn't exist.

Questions:

1. What to use for complicated 3d graphs? I tried Mathematica, but not sure how to combine two 3d graphs into one
2. Can anyone do Exercise 1. in Chapter 5 of Christianini's SVM book?
3. If we use Robinson's non-standard Analysis, could we sensibly define "uniform distribution over all integers"?
   

Resources:

• Dan Klein's "Lagrange Multipliers without Permanent Scarring" http://www-diglib.stanford.edu/~klein/lagrange-multipliers.pdf
• Chapter 5 of N. Cristianini and J. Shawe-Taylor Support-Vector Machines book http://www.support-vector.net/chapter_5.html
• Chapter 5 of Stephen Boyd and Lieven Vandenberghe "Convex Optimization" http://www.stanford.edu/~boyd/cvxbook.html
• Bertsekas, Dimitri P. "Constrained optimization and Lagrange multiplier methods" ISBN: 0120934809
  

Interesting blogs, newsgroups, chatrooms

Here are some things that someone who likes math, Machine Learning or statistics may find interesting

Technical:

• John Langford's blog -- http://hunch.net/ , high quality technical posts on Machine Learning
  
• Lance Fortnow's blog -- http://weblog.fortnow.com/ , Computational Complexity and related
  
• Notebooks -- http://www.cscs.umich.edu/~crshalizi/notebooks/ , a collection of resources from Cosma Shalizi
  
• Illinois Genetic Algorithms Laboratory (IlliGAL) -- http://illigal.blogspot.com/
  
• AI-complete -- http://ai-complete.blogspot.com/ low-traffic, but high quality AI blog
  
• Neurodudes -- http://www.neurodudes.com/ Neuro-biological standpoint
  
• Statistical Modeling, Causal Inference, and Social Science -- http://www.stat.columbia.edu/~cook/movabletype/mlm/
  
  
  
  

non-Technical:

• AI Knowledge (http://www.karmachakra.com/aiknowledge) -- non-technical AI-related
• Ernie's 3D Pancakes -- http://3dpancakes.typepad.com/ernie/ Jeff is a "computational geometer"
• "Occasional thoughts by physicist Michael Nielsen" -- http://www.qinfo.org/people/nielsen/blog/
• Ferndando Pereira's blog -- http://radio.weblogs.com/0100167/
• Language log -- http://itre.cis.upenn.edu/~myl/languagelog/
• Hanna Wallach is doing a PhD in Machine Learning -- http://www.srcf.ucam.org/~hmw26/join-the-dots/
• The Alpha and Omega -- http://mahalanobis.twoday.net/ interesting snippets from an economist
• Thesilog -- http://www.sologen.net/thesilog/ Amir does research in control theory

Newsgroups:

• comp.lang.ai
  
• comp.lang.ai.neural-nets
  
• sci.stat.math
  
• Machine Learning (http://groups-beta.google.com/group/Machine-Learning)
  

Mailing Lists:

• Connectionists (calls for papers, jobs): http://www.cnbc.cmu.edu/Resources/connectionists.shtml
• COLT mailing list (more calls for papers): http://mail.cs.uiuc.edu/mailman/listinfo/colt
• UAI mailing list (if you can get on it): http://www.auai.org/
  

Chatrooms:

• irc.freenode.org #MachineLearning
  

Finding Blogs:

After looking at "Referring Link" stats of people browsing this blog, I discovered two new ways of finding relevant blogs

• Go to http://blo.gs and search for "Machine Learning"
  
• Go to http://www.technorati.com/, search for Machine Learning related links, and it'll give you other blogs that have that link
  

I found a few people who came to this blog after searching for mentions of illigal.blogspot.com , and their IP's traced to Illinois, I wonder why ;)

Feel free to post other cool blogs, or other methods of finding them

Getting probabilities from students

A comment on Computational Complexity blog blog inspired me to look at the following problem

Suppose you give true/false test to students and want them to put down their subjective probabilities that answer is true/false. To make them honest, you would want to award points in such a way, that in order to maximize their expected points, the student would need to report their correct probabilities. Which utility function to use? It turns out, f(x)=A log x + B is one such family. Here's the derivation


Questions:
1) Does any other such utility function exist?
2) What are other fun ways to torture students?

Here are graphs of three possible functions that can be used for eliciting probabilities from students. They are all concave, maybe one can prove any suitable function must be concave?