
There are 9 independent sets.

Because the graphs are disjoint we could simplify the task by counting graphs in each connected component separately and multiplying the result
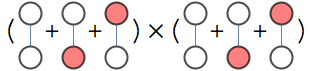
Variational approach is one way of extending this decomposition idea to connected graphs.
Consider the problem of counting independent sets in the following graph.

There are 7 independent sets. Let $x_i=1$ indicate that node $i$ is occupied, and $P(x_1,x_2,x_3,x_4)$ be a uniform distribution over independent sets, meaning it is either 1/7 or 0 depending whether $x_1,x_2,x_3,x_4$ forms an independent set
Entropy of uniform distribution over $n$ independent sets distribution is $H=-\log(1/n)$, hence $n=\exp H$, so to find the number of independent sets just find the entropy of distribution $P$ and exponentiate it.
We can represent P as follows
$$P(x_1,x_2,x_3,x_4)=\frac{P_a(x_1,x_2,x_3)P_b(x_1,x_3,x_4)}{P_c(x_1,x_3)}$$
Entropy of P similarly factorizes
$$H=H_a + H_b - H_c$$
Once you have $P_A$, $P_B$ and $P_C$ representing our local distributions of our factorization, we can forget the original graph and compute the number of independent sets from entropies of these factors
To find factorization of $P$ into $P_a,P_b$, and $P_c$ minimize the following objective
$$KL(\frac{P_a P_b}{P_c},P)$$
This is KL-divergence between our factorized representation and original representation. Message passing schemes like cluster belief propagation can be derived as one approach of solving this minimization problem. In this case, cluster belief propagation takes 2 iterations to find the minimum of this objective. Note that the particular form of distance is important. We could reverse the order and instead minimize $KL(P,P_a P_b/P_c)$ and while this makes sense from approximation stand-point, minimizing reversed form of KL-divergence is generally intractable.
This decomposition is sufficiently rich that we can model P exactly using proper choice of $P_a,P_b$ and $P_c$, so the minimum of our objective is 0, and our entropy decomposition is exact.
Now, the number of independent sets using decomposition above factorizes as
$$n=\exp H=\frac{\exp H_a \exp H_b}{\exp H_c} = \frac{\left(\frac{7}{2^{4/7}}\right)^2}{\frac{7}{2\ 2^{1/7}}} = \frac{4.75 \times 4.75}{3.17}=7$$
Our decomposition can be schematically represented as the following cluster graph

We have two regions and we can think of our decomposition as counting number of independent sets in each region, then dividing by number of independent sets in the vertex set shared by pair of connected regions. Note that region A gets "4.75 independent sets" so this is not as intuitive as decomposition into connected components
Here's another example of graph and its decomposition.


Using 123 to refer to $P(x_1,x_2,x_3)$ the formula representing this decomposition is as follows
$$\frac{124\times 236\times 2456 \times 4568 \times 478\times 489}{24\times 26 \times 456 \times 48 \times 68}$$
There are 63 independent sets in this graph, and using decomposition above the count decomposes as follows:
$$63=\frac{\left(\frac{21\ 3^{5/7}}{2\ 2^{19/21} 5^{25/63}}\right)^2 \left(\frac{3\ 21^{1/3}}{2^{16/21} 5^{5/63}}\right)^4}{\frac{21\ 3^{3/7}}{2\ 2^{1/7} 5^{50/63}} \left(\frac{3\ 21^{1/3}}{2\ 2^{3/7} 5^{5/63}}\right)^4}$$
Finding efficient decomposition that models distribution exactly requires that graph has small tree-width. This is not the case for many graphs, such as large square grids, but we can apply the same procedure to get cheap inexact decomposition.
Consider the following inexact decomposition of our 3x3 grid

Corresponding decomposition has 4 clusters and 4 separators, and the following factorization formula
$$\frac{1245\times 2356 \times 4578 \times 5689}{25\times 45 \times 56 \times 58}$$
We can use minimization objective as before to find the parameters of this factorization. Since original distribution can not be exactly represented in this factorization, result will be approximate, unlike previous two example.
Using message-passing to solve the variational problem takes about 20 iterations to converge, to an estimate of 46.97 independent sets

To try various decompositions yourself, unzip the archive and look at usage examples in indBethe3-test.nb
Notebooks
99 comments:
interesting post and nice examples!
Can you explain how you got $\exp H_a =\frac{7}{2^{4/7}}$ ?
To my understanding, the reason your first decomposition took only two iterations to reach the optimal solution, is because your cluster graph was actually a tree. Hence BP works like forward-backward and reaches the correct solution. Your other cluster graph is not a tree, and hence BP is just an approximation.
H_a is the entropy of the distribution over nodes 1,2,3. In other words it's the entropy with one node of the cycle marginalized out. Factor of 7 comes out because there are 7 outcomes before marginalization. Writing out the entropy explicitly you get
$$\frac{2}{7} \log \left(\frac{2}{7}\right)+\frac{1}{7} \log \left(\frac{1}{7}\right)+\frac{2}{7} \log \left(\frac{2}{7}\right)+\frac{1}{7} \log \left(\frac{1}{7}\right)+\frac{1}{7} \log \left(\frac{1}{7}\right)$$
To the other point -- yes -- for exact results, the cluster graph must be a junction tree. This also seems to also be a necessary condition for exactness if we allow more general belief propagation schemes -- http://stats.stackexchange.com/questions/4564/when-is-generalized-belief-propagation-exact
Thanks! I thought there was a trick in calculating this entropy without explicitly enumerating the outcomes.
Yaroslav,
From this example it seems that computing the entropy of a marginal is equally hard as computing the entropy of the joint distribution (or counting independent sets). If so, what's the point in such decomposition?
Roman -- to compute cluster entropy, you sum over all outcomes in a cluster, which scales exponentially with the size of the cluster. Brute force scales exponentially with size of the whole graph.
Yes, but for each cluster outcome one still needs to compute its probability w.r.t. the whole graph (either 1/7 or 2/7 in the example). Is there an efficient way to do this?
Indeed there is. You get marginals by solving KL-divergence optimization problem I described above. That objective can be evaluated in time that's only linear in size of the graph (exponential in size of cluster), and you can find local minimum efficiently. One approach gives Cluster BP, derivation on page 388-389 of Koller's book. When cluster graphs are trees like above, objective is convex and cluster BP update steps are identical to the junction tree algorithm, so you get exact result.
I see now. Thank you!
This is nice blog.
http://bwexports.in/products.php
super,so nice :))
Block Board Manufacturer in India
Hello, I saw a sphere image in your blog and linked to it in my blog. Is this okay or would you like it removed?
Regards,
Dave
@huer_innov
davehuer.com
the posting is here: http://davehuer.com/blog/is-globular-thinking-an-encryption-cypher/
Great post , this artivle is uniques and given greatful information ,Thanks for share this post . We are given Surplace ensures an on time service post sale, with the interference of their possess technical or in association with manufacturers to resolve any troubles. Please know more click Here Biesse woodworking machine
Hello your blog is sharing great information on this topic, we are providing spazzaneve, saldatrice inverter. Thanks for sharing this information.
This is great revealing content. Thank you I really appreciate the unique articles you write. remmtools provide this scarpe antinfortunistiche
KAMI SEKELUARGA MENGUCAPKAN BANYAK TERIMA KASIH ATAS BANTUANNYA MBAH , NOMOR YANG MBAH BERIKAN/ 4D SGP& HK SAYA DAPAT (350) JUTA ALHAMDULILLAH TEMBUS, SELURUH HUTANG2 SAYA SUDAH SAYA LUNAS DAN KAMI BISAH USAHA LAGI. JIKA ANDA INGIN SEPERTI SAYA HUB MBAH_PURO _085_342_734_904_ terima kasih.الالله صلى الله عليه وسلموعليكوتهله صلى الل
KAMI SEKELUARGA MENGUCAPKAN BANYAK TERIMA KASIH ATAS BANTUANNYA MBAH , NOMOR YANG MBAH BERIKAN/ 4D SGP& HK SAYA DAPAT (350) JUTA ALHAMDULILLAH TEMBUS, SELURUH HUTANG2 SAYA SUDAH SAYA LUNAS DAN KAMI BISAH USAHA LAGI. JIKA ANDA INGIN SEPERTI SAYA HUB MBAH_PURO _085_342_734_904_ terima kasih.الالله صلى الله عليه وسلموعليكوتهله صلى الل
KAMI SEKELUARGA MENGUCAPKAN BANYAK TERIMA KASIH ATAS BANTUANNYA MBAH , NOMOR YANG MBAH BERIKAN/ 4D SGP& HK SAYA DAPAT (350) JUTA ALHAMDULILLAH TEMBUS, SELURUH HUTANG2 SAYA SUDAH SAYA LUNAS DAN KAMI BISAH USAHA LAGI. JIKA ANDA INGIN SEPERTI SAYA HUB MBAH_PURO _085_342_734_904_ terima kasih.الالله صلى الله عليه وسلموعليكوتهله صلى الل
article very helpful at all, I personally really like, for that I can only say thank you for sharing and hopefully more successful in the future.
Agen Togel Online
Agen Bola SBOBET
Agen Domino QQ
Baccarat
Bandar Poker
Capsa Susun
Domino
Main Bandarq
Situs Game Bandarkiu
Situs Poker Asia
Prediksi Hasil4D
Film Bokep ABG
Bokep Online
Duniamaya
Way cool! Some extremely valid points! I appreciate you writing
this article and the rest of the website is also very good.
Salam Pramuka
Kita Banget
Thank you
http://makelartogel.com/
Agen Judi Bandar Sakong Samkong Online Terbesar Di Indonesia Dan Cara Bermain Di Android Download Apk
http://www.bandarsamkong.net/ / agen sakong
Hi there, I do believe your web site may be having internet browser compatibility issues.
When I look at your website in Safari, it looks fine however, if opening in IE, it's got some overlapping issues.
I simply wanted to provide you with a quick heads up!
Aside from that, fantastic site!
AGEN SAKONG
AGEN SAKONG ONLINE
BANDAR SAKONG
JUDI SAKONG
SAKONG ONLINE
AGEN BACCARAT ONLINE
BANDAR POKER DOMINOQQ
BANDARQ
Great post. I was checking continuously this blog and I am impressed!
Situs BandarQ Terpercaya 2017
Proses Cepat & Aman | Poker Online | Bandar Q Online | Domino QQ | Capsa | Adu QiuQiu | Bandar Sakong | Agen Judi Poker Mudah menangnya dengan Win Rate Tertinggi....!!
Join-->> Bandar Q
Kumpulan Berita Terupdate
Updaterus.Website
Situs Informasi Judi Online
InfoJudiOnline
Kumpulan Cerita Seks dan Video Bokep Terbaru 2017:
Cerita Sex
Video Bokep
article very helpful at all, I personally really like, for that I can only say thank you for sharing and hopefully more successful in the future.
coming to website :
http://bandarwebsiteqq.blogspot.com/2017/01/permainan-poker-online-selalu-menjadi.html
https://jokerqq99.tumblr.com/
http://bandarwebsite.angelfire.com/
bandarjoker.bravesites.com
bandarberita.jimdo.com
bandarjokerq.weebly.com
https://www.evernote.com/shard/s663/sh/4891efd3-6fa8-485f-a7c5-cb2aa471c2f1/0815372d230b1f7d9b227d15c0659f18
http://www.blogigo.com/trikjudi
http://xiaosad115.wixsite.com/bandarpoker
http://jokerqqinfo.wikidot.com/system:welcome
http://fourmjudi.webs.com/
jokerq.edublogs.org
doniidurmawan.deviantart.com
http://websitejudi.ucoz.org/news/cara_gampang_menang_bermain_permainan_bandar_sakong_online/2017-04-10-3
https://groups.google.com/forum/#!forum/jokerqqinfo
jokerqqinfo.sosblogs.com
http://logdown.com/account/posts/1366616-tips-jitu-permainan-poker-online-di-judi-online-indonesia/preview
http://donnidurmawan.inube.com/blog/5657257/memainkan-judi-domino-online-dengan-bagus-dan-menang/
http://beritajudi.page.tl/
https://storify.com/donnidurmawan/jokerqq-situs-judi-online
http://bandarqiu.jigsy.com/
http://judionline.onesmablog.com/Belajar-mengenal-permainan-Bandar-Poker-Online-Indonesia-6083624
http://bandarjudi.manifo.com/
http://donnidurmawan.emyspot.com/
https://jokerqq99.tumblr.com/post/158344652081/capsa-susun-permainan-judi-online-terseru-di-indonesia
https://trikjudi.joomla.com/
http://bandarwebsiteqq.blogspot.com/2017/05/trik-ampuh-menang-bermain-permainan.html
http://bandarwebsiteqq.blogspot.com/2017/05/cara-gampang-menang-bermain-permainan.html
http://bandarwebsiteqq.blogspot.com/2017/05/trik-ampuh-menang-bermain-permainan.html
http://bandarwebsiteqq.blogspot.com/2017/05/cara-gampang-menang-bermain-permainan.html
http://forumjudi.bravesites.com/berita-sakong
http://forumjudi.bravesites.com/berita-joker
http://beritajudi.emyspot.com/pages/cara-bermain-permainan-bandar-sakong-online-indonesia.html
http://bandarjudi.cabanova.com/
http://bandarjudi.moonfruit.com/home/4593876110?preview=Y
http://bandarjudi.moonfruit.com/home/4593876110?preview=Y
http://kiritokunz.blog.fc2.com/blog-entry-1.html
http://www.trikjudi.sitew.org/#Accueil.A
https://maniapoker.yolasite.com/
Looking forward to reading more. 've been trying for a while but I never seem to get there! Great article post.Really thank you! Much obliged.
poker online
bandar kiu kiu
bandar qq
domino qq
Agen Poker Online
Judi Poker Online
Situs Poker Online
Cerita Sex Tante
Video Bokep Indonesia
Video Bokep Jepang
Situs Agen Judi Game QQ Online Terbaik dan Terpercaya dan Download Game QQ online APK
qq online
Agen Judi Game Bandar DominoQQ, Agen DominoQQ, Domino Online dan Download Game domino APK
dominoqq
Thanks For Share This Article, Really Awesome Dude...
Situs Poker Online
Situs Domino QQ
Situs Judi Poker
Situs Bandar QQ
Agen Domino QQ
Poker Online
Agen Poker Online
Situs Poker Online
Agen Judi Poker
Judi Domino QQ
Agen Bandar QQ
Poker Online
"Salam super MGMPOKER88 the best of poker online...
KEPUASAN ANDA ADALAH KEBANGGAAN KAMI..!!!
Cobalah permainan kartu terbaik diindonesia www,dompetmgm,com
Hanya modal Rp. 20,000 Bisa dapatkan jutaan hinggan puluhan juta
Sudah banyak member mgmpoker88 yang memenangkan uang puluhan juta..
Ayo ikutan main dan menangkan JACKPOT Ratusan JUTA hanya di mgmpoker88.com
MGMPOKER88
Mari gabung dan daftarkan diri anda sekarang juga dan ajak teman kamu bermain dengan menggunakan referal kamu dan dapatkan keuntungan sebanyak 20% dari teman kamu dan kami juga memberikan bonus cashback sebanyak 0.5% dan untuk tingkat kemenangan di website mgmpoker88 adalah 99% dan karena yang bermain adalah player semuanya dan tidak ada sistim komputerisasi (Fair Play).
Untuk Info Lebih Lanjut Bisa Saja Langsung Hubungi Costumer Service kami di :
LiveSupport 24JAM.
◙ LIVE CHAT : www,mgmdomino,com
◙ Pin BBM : D8BCE200...
◙ Line : +855968725318
◙ Skype : MGM POKER88"
This is a very well written post. I will be sure to bookmark it and return to read more of your beneficial information.
Video Porno Jepang
Video Mesum Jepang
many articles provide important and inspiring information thankspoker online
BOKEP JAPANESE HD
BOKEP HD BARAT
BOKEP HD INDO
BOKEP INDO HD
Situs Agen Judi Dewa Poker Online Terpercaya Indonesia Dengan Jackpot Terbesar yang dapat dimainkan melalui android atau IOS Iphone dengan menggunakan uang asli indonesia
KUMPULAN SITUS TERPERCAYA
Poker Online Terpercaya
Situs Judi Online
Freebet
Cerita Seks
Streaming Bokep
PROMO TERBARU!!
1. Welcome Bonus New Member 20%
2. BONUS DEPOSIT SETIAP HARI
3. BONUS TURN OVER Up to 0.5%
4. BONUS REFFERAL 10% SEUMUR HIDUP
5. HADIAH JACKPOT PULUHAN JUTAAN RUPIAH
Untuk Info Lebih Lanjut
Silahkan Hubungi Kami Di :
- Live chat (www•kartugadis•com )
- Whatsapp : +855966624192
- BBM : D8C893A4
- Line : gadispoker-cs
SALAM KEMENANGAN DAN HOKI UNTUK PARA MEMBER GADISPOKER
Artikel yang sangat menarik. saya mendapat banyak informasi disini! terimakasih gan lanjutkan lagi ya ditunggu informasi berikutnya.
Lxgroup
SENANG DOMINO
SITUS DOMINO ONLINE TERPERCAYA
DEPOSIT MENGGUNAKAN PULSA
Bonus TurnOver 0.5% (Dibagikan Setiap Hari Senin)
Bonus Referal 20% (10% Otomatis & 10% Manual)
Minimal Deposit Rp. 10.000
wechat : goyangpoker
Line : 85581259896
No hp : +85581259896
Whatsapp : +85581259896
BB : 559518E4
Baca juga tips dan trik bermain judi online
situs poker online poker online Indonesia
SENANG DOMINO
SITUS DOMINO ONLINE TERPERCAYA
DOMINO ONLINE
Bonus TurnOver 0.5% (Dibagikan Setiap Hari Senin)
Bonus Referal 20% (10% Otomatis & 10% Manual)
Minimal Deposit Rp. 10.000
wechat : goyangpoker
Line : 85581259896
No hp : +85581259896
Whatsapp : +85581259896
BB : 559518E4
Baca juga tips dan trik bermain judi online
situs poker online poker online Indonesia
♥♦♣♠ VIP DOMINO ♠♣♦♥
Sudah TERBUKTI !!
Hanya di VIPDOMINO Lebih Mudah Menangnya.
Dengan WINRATE KEMENANGAN TERTINGGI
Raih KEMENANGAN SEBESAR-SEBESARNYA Bersama Kami!
8 GAME IN USER ID 1 :
- Domino99
- BandarQ
- Poker
- AduQ
- Capsa Susun
- Bandar Poker
- Sakong Online
- Bandar66
Nikmati Bonus-Bonus Melimpah Yang Bisa Anda Dapatkan Di
Situs Kami VIPDOMINO Situs Resmi, Aman Dan
Terpercaya ^^ Keunggulan VIPDOMINO :
- Rating Kemenangan Terbesar
- Bonus TurnOver Atau Cashback Di Bagikan Setiap 5
Hari 0.3%
- Bonus Referral Dan Extra Refferal Seumur Hidup 15%
- Minimal Deposit Hanya Rp20.000,- & Withdraw Rp20.000,-
- Tidak Ada Batas Untuk Melakukan Withdraw/Penarikan
Dana
- Pelayanan Yang Ramah Dan Proses Deposit / Withdraw Cepat
- Dengan Server Poker-V Yang Besar Beserta Ribuan pemain
Di Seluruh Indonesia,
- NO ADMIN , NO ROBOT 100% Player Vs Player
Fasilitas BANK yang di sediakan :
- BCA
- Mandiri
- BNI
- BRI
- Danamon
- Permata
- Panin
- Sakong Online
Ambil Gadgetmu Dan Bergabung Bersama Kami
Untuk info lebih jelas silahkan hubungi CS kami :
BBM : D8EB96DA
WA : : +62 852-5967-8372
LINE : INDOVIP88
Link Alternatif Kami :
IndoVip88 (.) Com
IndoVip303 (.) Com
SakongVip (.) Com
SENANG DOMINO
SITUS DOMINO ONLINE TERPERCAYA
JUDI POKER
Bonus TurnOver 0.5% (Dibagikan Setiap Hari Senin)
Bonus Referal 20% (10% Otomatis & 10% Manual)
Minimal Deposit Rp. 10.000
wechat : goyangpoker
Line : 85581259896
No hp : +85581259896
Whatsapp : +85581259896
BB : 559518E4
Baca juga tips dan trik bermain judi online
situs poker online poker online Indonesia
SENANG DOMINO
AGEN POKER ONLINE
DEPOSIT PULSA
Bonus TurnOver 0.5% (Dibagikan Setiap Hari Senin)
Bonus Referal 20% (10% Otomatis & 10% Manual)
Minimal Deposit Rp. 10.000
wechat : goyangpoker
Line : 85581259896
No hp : +85581259896
Whatsapp : +85581259896
BB : 559518E4
Baca juga tips dan trik bermain judi online
situs poker online poker online Indonesia
Excellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
situs judi slot online terpercaya & daftar game mesin slot online uang asli terbaik & terbesar di Indonesia. ✅ Bandar tembak ikan Joker123
https://taruhanslot.net/situs-online-judi-slot-terbaik-joker123/
Link Official Bolavita : http://159.89.197.59/
Telegram : +62812-2222-995
Wechat : Bolavita
WA : +62812-2222-995
Line : cs_bolavita
situs agen judi slot online terpercaya
daftar joker123
Joker123
data sgp
joker123 slot
Joker123
Joker123
http://jokerindo99.com/
sgdtoto cashback togel
sgdtoto cashback livegames
sgdtoto deposit 24jam online
sgdtoto
sgdtoto deposit pulsa
sgdtoto togel livegames
I like your post and all you share with us is up to date and quite informative, I would like to bookmark the page so I can come here again to read you, as you have done a wonderful job.
prediksi togel
iPads
Thanks for Fantasctic blog and its to much informatic which i never think ..Keep writing and grwoing your self
trusted gambling place at this time
벳365코리아
크레이지슬롯
크레이지슬롯
릴게임사이트
슬롯게임
카지노사이트
카지노사이트
벳365코리아
파워볼사이트
블랙존사이트
BET365코리아
https://ocn2001.com/
Hello Kami Ingin Mengajak Anda.
Mencoba Bermain 9 Game Terbaik Dengan Winrate Tertinggi 100% Di Jamin.
Daftar Disini : MejaQQ
Daftar Disini : QQ Online
در مورد این چند سوال نمی توان نظری قطعی اعلام کرد که کدام برند
درب ضد سرقت
ایرانی بهترین برند درب ضد سرقت ایران در بین تولید کنندها درب ضد سرقت می باشد
Situs Poker Uang Asli
Situs Poker 24 Jam
Situs Poker Indonesia
MEJAQQ: AGEN JUDI POKER DOMINOQQ BANDARQ ONLINE TERBESAR DI ASIA
MEJAQQ
BANDARQ ONLINE
SITUS BANDARQ
WOW! very imformative post.
I surely recommend this to all my friends.
Keep posting this kind of awesome blog!
kindly click our link below.Thankyou
안전놀이터
https://pmx7.com/ 안전놀이터
I love these blog! They are adorable! Please click and visit our website :)
카지노사이트
https://yhn777.com 카지노사이트
Sakurapoker juga memberikan kemudahan bertransaksi seperti deposit 24 jam semua bank seperti bca, bni, mandiri, bri dan cimb. Semua transaksi akan diproses tanpa adanya jam offline, transaksi tidak akan diproses jika posisi bank sedang gangguan.
Support Deposit Poker Online OVO, Gopay, Dana dan Link
This is a nice site ,keep it up and visit our website too.
Https://yhn876.com 카지노사이트
This Post is providing valuable and unique information, I know that you take a time and effort to make a awesome article 먹튀검증
This Post is providing valuable and unique information, I know that you take a time and effort to make a awesome article 파워볼전용사이트
This article gives the light in which we can observe the reality. This is very nice one and gives indepth information. Thanks for this nice article 메이저사이트
나는 여기서 몇 가지 좋은 것들을 배웠다. 다시 방문하기 위해 북마크 할 가치가 있습니다. 이런 종류의 환상적인 유익한 웹 사이트를 만들기 위해 얼마나 많은 노력을 기울 였는지 놀랍습니다. 안전사이트
It was thinking about whether I could utilize this review on my other site, I will connect it back to your site though.Great Thanks. 먹튀폴리스
I appreciate several from the Information which has been composed, and especially the remarks posted I will visit once more. 먹튀
I should say only that its awesome! The blog is informational and always produce amazing things. casino24
https://twitter.com/totobobbi Easily, the article is actually the best topic on this registry related issue. I fit in with your conclusions and will eagerly look forward to your next updates. 토토사이트
Superbly written article, if only all bloggers offered the same content as you, the internet would be a far better place. 이기자벳
https://twitter.com/totobobbi I absolutely adore this information as this is going to be very difficulty time for the whole world. great things are coming for sure 토토사이트
looking for site that you really love?
here, come and visit our site
just click the link below. Thank you!
안전놀이터
https://pmx7.com/ 안전놀이터
I can see that you are an expert at your field! I am launching a website soon, and your information will be very useful for me .. Thanks for all your help and wishing you all the success in your business 먹튀검증
I really enjoyed reading your blog, you have worked very well on this website but also I like it and I have received a lot of suggestions in your web site and I have learned all about it and I have been benefited from writing such blogs. ….. 먹튀폴리스
I truly appreciate this post. I’ve been looking all over for this! Thank goodness I found it on Bing. You have made my day! Thank you again! 먹튀검증
I have to thank you for the efforts you have put in penning this blog. I really hope to view the same high-grade content by you in the future as well. In fact, your creative writing abilities has inspired me to get my very own blog now 토토사이트
Greetings! Very helpful advice within this article! It is the little changes that will make the greatest changes. Thanks for sharing! 토토사이트
"interesting blog thanks to this type fashion blog
" 안전놀이터
"Nice blog here! Also your website loads up very fast!
What host are you using? Can I get your affiliate
link to your host? I wish my website loaded up as fast as
yours lol" 메이저놀이터
I am extremely impressed with your writing skills and also with the layout on your blog. Is this a paid theme or did you modify it yourself? Either way keep up the nice quality writing, it is rare to see a nice blog like this one nowadays.. 안전놀이터
I’m typically to running a blog and i actually recognize your content. The article has really peaks my interest. I’m going to bookmark your web site and maintain checking for brand spanking new information. 토토사이트
A very awesome blog post. We are really grateful for your blog post. You will find a lot of approaches after visiting your post. 먹튀폴리스
A very awesome blog post. We are really grateful for your blog post. You will find a lot of approaches after visiting your post. 먹튀폴리스
Its a great pleasure reading your post.Its full of information I am looking for and I love to post a comment that «The content of your post is awesome» Great work. 슈어맨
"Hurrah! After all I got a weblog from where I can really get useful information regarding my study and knowledge.
" 슈어맨
Yes i am totally agreed with this article and i just want say that this article is very nice and very informative article.I will make sure to be reading your blog more. You made a good point but I can't help but wonder, what about the other side? !!!!!!THANKS!!! 온라인카지노
"If you are going for best contents like me, only go to see this
web page all the time because it offers feature contents, thanks" 토토사이트
Its a great pleasure reading your post.Its full of information I am looking for and I love to post a comment that «The content of your post is awesome» Great work. 바카라사이트
I like what you guys are up also. Such smart work and reporting! Keep up the superb works guys I’ve incorporated you guys to my blogroll. I think it’ll improve the value of my website :). 먹튀검증
It is really what I wanted to see hope in future you will continue for sharing such a excellent post. 안전놀이터
"Your style is so unique in comparison to other people I’ve read stuff from. Many thanks for posting when you’ve got the opportunity, Guess I’ll just bookmark this page.
" 먹튀폴리스
Great piece of info, I'm excited to read more article. Keep it up
my friend! Please visit our site too.
카지노사이트
https://yhn777.com 카지노사이트
Very likely I’m going to bookmark your blog . You absolutely have wonderful stories. Cheers for sharing with us your blo 토토사이트
The post is written in very a good manner and it contains many useful information for me 먹튀폴리스
Hiya, I am really glad I’ve found this information. Nowadays bloggers publish just about gossips and net and this is really frustrating. A good site with exciting content, this is what I need. Thanks for keeping this website, I will be visiting it. Do you do newsletters? Can’t find it. 먹튀검증
We are a group of volunteers and starting a new scheme in our community. 먹튀검증
KAPAL ASIA (KAPAL JUDI)
HOT PROMO :
- Bonus Cashback Mingguan Hingga 15%
- Bonus Refrensi 2,5% Seumur Hidup
- Bonus Rollingan Casino 0.8%
- Bonus Rollingan Mingguan Sportbook Refferal 0,1%
- Bonus Rollingan Poker 0.2%
Discount 4D : 66.00% , 3D : 59.5.00% , 2D : 29.5.00%
Kombinasi = 5%
Shio = 12%
Colok Angka (1A) = 5%
Colok Macau (2A) = 15%
Colok Naga (3A) = 15%
Colok Jitu = 8%
jika ada kendala silahkan hubungi ke live chat kami ya bosku ^^
kami siap membantu bosku 24jam :)
di tunggu kedatangan nya kembali bosku ^^
WA: +62 852-3676-6236 KAPALJUDI
Fanspage : Kapal Asia Indonesia
IG : KapalAsiaHoki
Www BetKapal Com
JUDI ONLINE TERPERCAYA
BET88
88BET
BOLA88
SLOT88
SBOBET88
SLOT ONLINE
BET88
88BET
SLOT ONLINE
SLOT ONLINE
SLOT ONLINE
BOS717
CASINO ONLINE
AGEN TOGEL TERLENGKAP
SLOT ONLINE
QQSLOT ONLINE
JUDI CASINO ONLINE
SBOBET WAP
SLOT ONLINE
CASINO ONLINE
BET88 ONLINE
BET88
BET88
CASINO SBOBET88
AGEN SBOBET88
SITUS JUDI ONLINE
JUDI SLOT ONLINE
AGEN TOGEL
SLOT ONLINE
CASINO ONLINE
AGEN BOLA
Tembak Ikan Online
TOGEL ONLINE
SLOT ONLINE
QQGO 368BET
BET88
SITUS JUDI DEPOSIT PULSA
AGEN BETTING ONLINE
AGEN JUDI CASINO ONLINE
BANDAR JUDI CASINO
BET88
BET88
88BET
BET88 ONLINE
88BET
88BET
BET88
88BET
BET88 ONLINE
Situs Online Terbesar, Terlengkap Dan Terpercaya
Aslijudi
Prediksi Parlay
NowGoal
Asligacoronline
Kunjungi Juga Blog Kami Lainnya
Aslislotonline.blogspot.com
Aslijudibola.blogspot.com
Aslilivecasino.blogspot.com
Aslisituspokeronline.blogspot.com
Aslisabungayam.blogspot.com
very nice post, i certainly love this website, keep on it . I’m impressed, I must say. Genuinely rarely will i encounter a weblog that’s both educative and entertaining, and let me tell you, you could have hit the nail about the head. Your concept is outstanding; the catch is something that not enough folks are speaking intelligently about. I am very happy which i found this at my seek out some thing concerning this. I discovered your this post while taking a gander at for some related information on blog search...It's a not all that horrendous post..keep posting and invigorate the information. 먹튀검증
I simply want to tell you that I am new to weblog and definitely liked this blog site. Very likely I’m going to bookmark your blog . You absolutely have wonderful stories. Cheers for sharing with us your blog. This content is simply exciting and creative. I have been deciding on a institutional move and this has helped me with one aspect. Excellent read, Positive site, where did u come up with the information on this posting?I have read a few of the articles on your website now, and I really like your style. Thanks a million and please keep up the effective work. Thank you for such a good post. Keep sharing wonderful posts like this. I will be checking back soon. 먹튀폴리스주소
I have bookmarked your website because this site contains valuable information in it. I am really happy with articles quality and presentation. Thanks a lot for keeping great stuff. I am very much thankful for this site. I have been searching to find a comfort or effective procedure to complete this process and I think this is the most suitable way to do it effectively. I think I have never seen such blogs ever before that has complete things with all details which I want. So kindly update this ever for us. Such an amazing and helpful post this is. I really really love it. It's so good and so awesome. I am just amazed. I hope that you continue to do your work like this in the future also. 먹튀사이트
Mudah Bermain Slot Android Online Di Daftar AHLIBET88 Karena Didukung Teknologi Yang Canggih
This is also a very good post which I really enjoyed reading. Thank you for sharing. A 60Hz refresh rate is probably sufficient for the majority of people if you simply use your monitor for work-related purposes. Nevertheless, adopting a faster refresh rate display has advantages because it makes the system feel more snappy and slick. Read in detail about Importance of Refresh rate.
"“We accept the love we think we deserve.”
" 무료웹툰
Post a Comment