$$\sum_{x_1,x_2,x_3} \exp(x_1 + x_2 + x_3)=\sum_{x_1} \exp x_1 \sum_{x_2} \exp x_2 \sum_{x_3} \exp x_3$$
This breaks the original large sum into 3 small sums which can be computed independently.
A more realistic scenario requires factorization into overlapping parts. For instance take the following
$$\sum_{x1,x2,x3,x_4,x_5} \exp(x_1 x_2 + x_2 x_3 + x_3 x_4+x_4 x_5)$$
You can't use directly apply distributive law here. Naive evaluation of the sum is exponential in the number of variables, however this problem can be solved in time linear in the number of variables.
Consider the following factorization
$$\sum_{x1,x2} \exp x_1 x_2 \left( \sum_{x_3} \exp x_2 x_3 \left( \sum_{x_4} \exp x_3 x_4 \left( \sum_{x_5} \exp x_4 x_5 \right) \right) \right) $$
Now note that when computing inner sums, naive approach results in same sum being recomputed many times. Save those shared pieces and you get an algorithm that's quadratic in number of variable values and linear in number of variables
Viterbi and Forward-Backward are specific names of this kind of dynamic programming for chain structured sums as above.
To consider tree-structured sum, take a problem of counting independent sets in a tree-structured graph. In this case we can use the following factorization
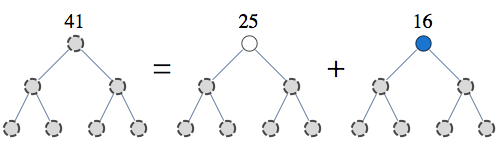
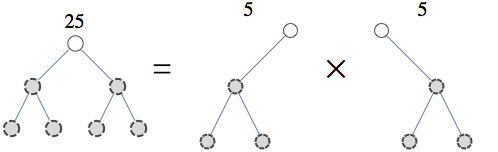
This is the first step of the recursion and you can repeat it until your pieces have tractable size.
Now for a general case of non-tree-structured graph, consider the sum below
$$\sum_{x1,x2,x3,x_4,x_5} \exp( x_1 x_2 + x_2 x_3 + x_3 x_4+x_4 x_5 + x_5 x_1 )$$
Here, variables form a loop, so regular tree recursion like Viterbi does not apply. However, this sum can be found efficiently, linear in the number of variables, and cubically in the number of variable values. I have more in depth explanation of decomposing problems like above in an answer on cstheory site but the basic idea is similar to the approach with independent sets -- fix some variables and recurse on subparts.
This kind of general factorization has been re-invented many times and is known as Generalized Distributive Law, tree-decomposition, junction tree, clique tree, partial k-tree, and probably a few other names.
Notebook
18 comments:
THANKS FOR THE INFORMATION...
<a href="http://www.chloros.in/digital-marketing-internship.htmlhttp://www.chloros.in/digital-marketing-internship.html>Digital Marketing Internship Program in Bangalore</a>
Great Article
IEEE final year projects on machine learning
JavaScript Training in Chennai
Final Year Project Centers in Chennai
JavaScript Training in Chennai
I think that service Coronavirusessay is the best in writing essay in this niche. Thank you!دانلود آهنگ قدیمی
دانلود آهنگ غمگین
با تبلیغات محیطی در اتوبان های پرتردد می توانید محصولات خود را به بخش بزرگی از افراد جامعه معرفی کنید.
This is a really decent site post. Not very numerous individuals would really, the way you simply did. I am truly inspired that there is such a great amount of data about this subject have been revealed buy marketing assignment online and you've put forth a valiant effort, with so much class. On the off chance that needed to know more about green smoke surveys, than by all methods come in and check our stuff.
I believe this will help your website become more organized because you have decided to set a part on this site for the inquiries regarding tax and as well as the helpful discussions. To be honest, this is one of the few sites that are doing this kind of strategy. Also, I think that this will not only benefit your clients or the potential ones but you most help with assignment writing especially because you will be able to see the questions easier.
If we are going to talk about murals, it is a harsh reality that there are people who do not appreciate artworks like this. I fell bad, but there is less that I can do; I want them to realize that murals are beautiful and worth appreciating. But I simply don't know where to start. Sometimes, I think of writing as my way to influence people to appraiser things that should be appreciated. I don't know if that is going to be effective, but I want to give it assignment crux uk a try.
Thank you for the informative post. It was thoroughly helpful to me. Keep posting more such articles and enlighten us.
python internship | web development internship |internship for mechanical engineering students |mechanical engineering internships |java training in chennai |internship for 1st year engineering students |online internships for cse students |online internship for engineering students |internship for ece students |data science internships
اجاره خودرو تهران
buy your underwear from zirpush
I appreciate the balanced approach you’ve taken here. If you're struggling with slow clicking, a CPS Test can help identify weaknesses and guide your improvement strategy.
I appreciate your hard work for writing this awesome article.
a lot of useful facts that is useful in our life. Thanks
Thank you a lot for giving everyone remarkably memorable
possibility to read from this web site
I am very enjoyed for this blog. Its an informative topic.
It help me very much to solve some problems.
I was diagnosed with Parkinson’s disease four years ago. After traditional medications stopped working, I tried a herbal treatment from NaturePath Herbal Clinic Within months, my tremors eased, balance improved, and I regained my energy. It’s been life-changing I feel like myself again. If you or a loved one has Parkinson’s, I recommend checking out their natural approach at [www.naturepathherbalclinic.com]. info@naturepathherbalclinic.com
Post a Comment