Junction trees in numerical analysis

There's a neat connection between Cholesky factorization and graph triangulations -- graph corresponding to Cholesky factorization of a sparse matrix is precisely the triangulation of the sparse matrix (when viewed as a graph) using canonical elimination ordering.

Here's an example of a matrix (corresponding to the graph with black edges only), and its Cholesky factorization. We triangulate the graph by any pairs of neighbors of v which have higher index than v, for every v. Extra edges added in this way correspond to extra non-zero entries in Cholesky decomposition of the original matrix. Different color edges/matrix entries correspond to non-zero entries in Cholesky factorization not present in original matrix



Furthermore, junction tree we get using min-fill heuristic of a graph is same structure as what is used to perform Cholesky factorization using parallel multi-frontal method

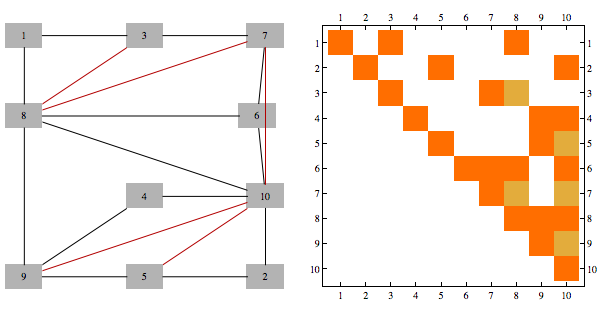
Here's a chordal matrix in perfect order and its Cholesky factorization


The fact that Cholesky factorization has the same sparsity structure as the original matrix confirms that its a chordal matrix in perfect elimination order

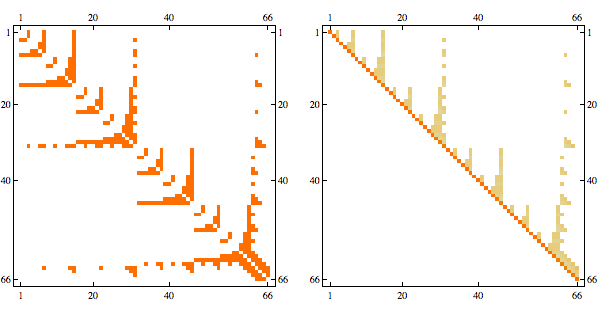
Here's the graph representation of the matrix


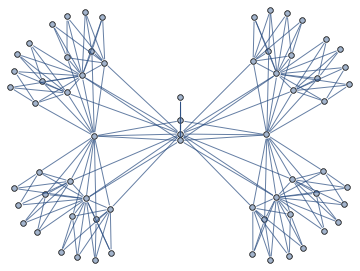
Junction tree decomposition of this graph reveals the following clique structure


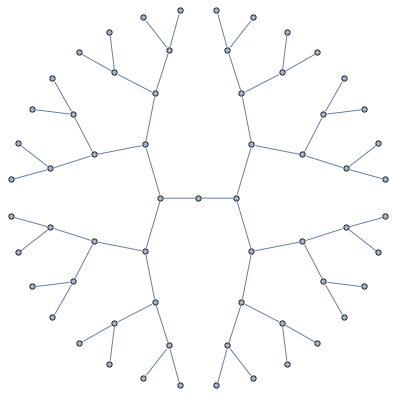
High branching structure of decomposition means that Cholesky factorization can be highly parallelized, in particular, the very last step of Cholesky decomposition of this matrix in minfill order consists of 32 independent tasks that can be done in parallel.

I packaged together some Mathematica code for these kinds of tasks