Positive-definite/negative-definite

Concepts of positive definite matrices and positive definite operators often come up in Machine Learning, here are some movies I made to visualize linear transformations corresponding to some common types of matrices:

Symmetric and positive definite







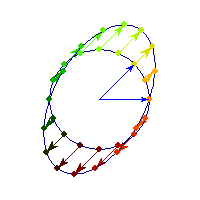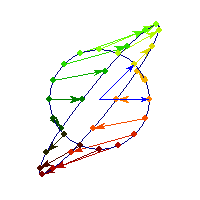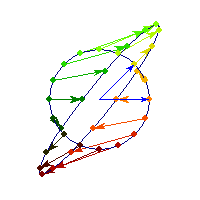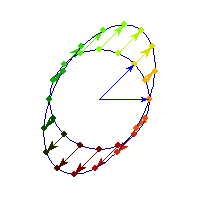
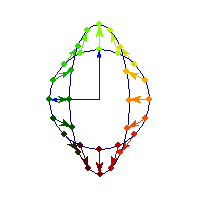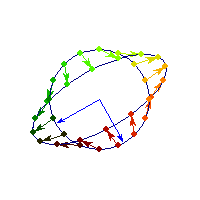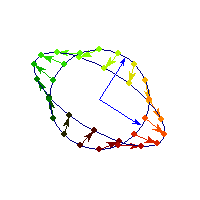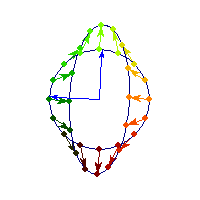
Symmetric positive definite matrices can be thought of matrices that stretch or shrink the circle along the eigenvectors (marked in blue).

The angle between x and Ax is always less than Pi/2, so x'Ax>0 forall x.

Symmetric and negative definite


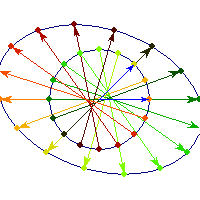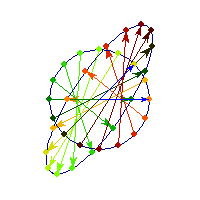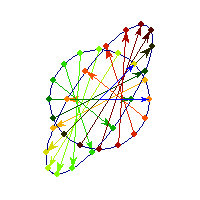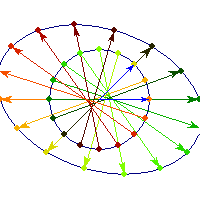
You can see in addition to stretching, every vector is flipped across the origin. So the angle is always between Pi/2 and Pi, hence x'Ax<0>0 and for others x'Ax


Symmetric and indefinite



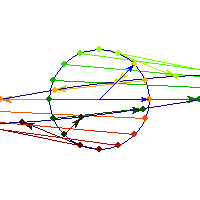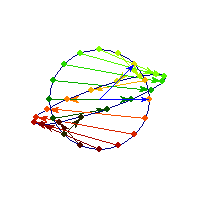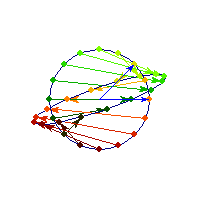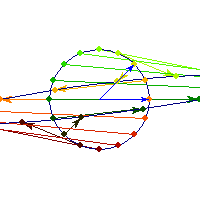
Vectors are flipped across one axis only, so sometimes the angle is more than Pi/2 and sometimes it's less. A quadratic form corresponding to such matrix will have a saddle point (you can see this because x'Ax will be positive along some directions, and negative along others)

Positive definite but not symmetric

Rotation by less than Pi/2 and positive skew are positive definite operations, even though they are not symmetric or diagonalizable.











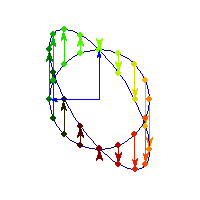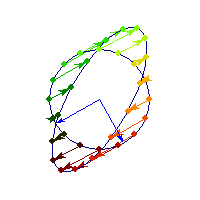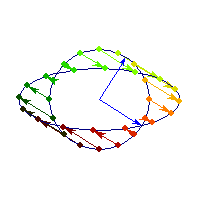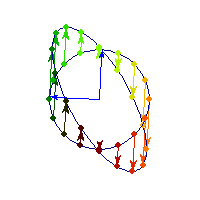
You can see in the first case there's only one vector (0,1) that does't change direction after action by A, so there's only 1 eigenvector, hence the matrix is not diagonalizable. In the second case, every vector changes after action by A so there are no (real) eigenvectors, and matrix is again not diagonalizable.