For instance consider unit sphere (radius 1)

If you go from 2 dimensions to 3 dimensions, the volume increases (Pi to 4/3 pi). Similar increase happens when you go to 3,4,5 dimensions. But then the volume starts to decrease. Eventually it decreases all the way to 0.
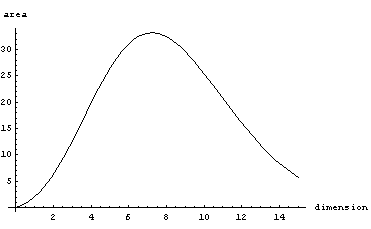
Now consider a cube of width 1. As dimension increases, the volume stays the same. But the length of the main diagonal grows as sqrt(dimension). So the corners become situated further and further away from the center, and eventually almost all the mass is concentrated in the corners (meaning outside of the inscribed sphere)
Here's a plot of the fraction of the mass concentrated in the corners as a function of dimension
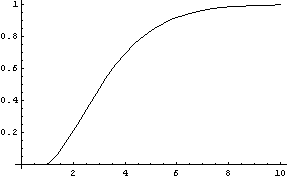
For a 7 dimensional cube, about 96% of the mass is concentrated in one of it's 128 "corners", so if we had 7 dimensional vision, we might see that cube like this

Finally consider what happens with a d-dimensional standard normal (unit covariance matrix, centered at 0). If we plot probability mass contained around a thin shell of radius r as a function r we get the following graphs (d=1,d=4,d=16)
The mean of this distribution is
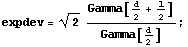
which can be approximated as sqrt(d)
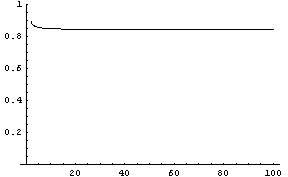
Furthermore you can derive that variance of this distribution converges to 1/2 (see notebook). Applying Chebyshev's inequality, we get that for any dimension, at least 0.75 of the mass is contained in the shell of thickness 1 centered at about sqrt(d). In numerical integration this seems to converge to a slightly higher number, for instance for 10^6 dimensions, it's about 0.84
Here's the Mathematica notebook with some derivations (web version)
14 comments:
Very interesting read. May I recommend the nice overview of Mario Koppen as complementary reading. damien
This is the math post of the year!
Nice post.
I have some sort of knee-jerk reaction against comparing the volume of spheres in different dimensions. What does it mean to compare the volume of something in 3d with units [L^3] and 4d with units [L^4]? I wouldn't like to say that one is ‘bigger’ than the other. Of course one may compare dimensionless quantities, which I appreciate is what you are doing by comparing the ratio of the volume of the sphere and the enclosing cube. One could also compare to an inscribed cube and see how all of the mass of the sphere gets pushed out to its surface, just as the cube’s mass goes to the corners.
A pratical application that spends some time working out how spheres and cubes fit together in high dimensions is http://tinyurl.com/s8xms
PS Damien I liked your link. Thanks.
Thanks for the link Damien, thanks for the comment Daniel, Iain -- I agree, units are not really meaningful.
Consider a cube with side 1 meter long. As dimensions increase, cube volume stays constant, goes to infinity or to zero depending on whether you use meters, millimeters or kilometers to measure volume.
Relative volume of cube inscribed in a sphere is another interesting calculation -- since diagonal^2 has length dx^2, where x is the length of the side, inscribed cube's "volume" goes down as d^{-d/2} which is faster than the rate at which sphere's volume decreases (about (d/2)^(-d/2))
Really nice !
As regards the gaussian part of this post, some graphs are missing ("following graphs d=1,d=4,d=16") and that makes "The mean of this distribution is..." a little confusing because you actually refer to E[||X||] and not to E[X] (which is always 0). This is obvious, but, at first glance I was confused...
Nevertheless, are there consequences on technics using d-normal (like Parzen estimator) ?
And what about the mass repartition of other distributions, with lower/bigger tails ?
Dear all, high-dimensional data analysis is the topic of my PhD thesis, which I am currently writing. I have gathered quite a few references about 'strange' properties of high dimensional spaces. If you are interested, just send me an email. damien
Nice introduction of simple math, high dimensional space seems to be challenging for we 3D human being. Anyway, really nice post and thanks.
Excellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
While browsing internet i came across your blog. Really ავეჯის გადაზიდვა found some good stuff here. I wanted some help from you. I am currently learning machine learning subject.
Navigate the Curse of Dimensionality with finesse in Machine Learning, as mastering its depths is the ultimate fnaf game of the data realm. Uncover hidden insights amidst complexity, leveraging algorithms akin to survival tactics against overwhelming odds.
The Curse of Dimensionality reveals how intuition falters as dimensions rise, much like in Cookie Clicker where adding cookies can create unexpectedly complex strategies.
Now consider a cube of width 1. As dimension increases, the volume stays the same. But the length of the main diagonal grows as sqrt(dimension). So the corners become situated further and further away from the center, and eventually almost all the mass is concentrated in the corners (meaning outside of the inscribed sphere)
accessing mentorship and guidance
dealing with failure and setbacks
Welcome to the ultimate Papa’s Freezeria guide, your complete resource for mastering one of the most beloved time management games ever created. In Papa’s Freezeria, precision, rhythm, and strategy combine to create a delicious challenge. Your mission? Craft flawless sundaes, serve customers efficiently, and earn big tips to grow your shop. Whether you’re a new employee or a seasoned pro aiming for five-star perfection, this step-by-step guide will help you dominate every day behind the counter.
Why Papa’s Freezeria Remains a Classic
papas freezeria continues to captivate players with its smooth gameplay loop that rewards both speed and accuracy. Each new day introduces:
Fresh ingredients that expand your menu.
More demanding customers with higher expectations.
Tight timing windows that test your multitasking skills.
The result? A fun yet challenging experience where mastery comes from balancing precision and speed—one sundae at a time.
Mastering the Four-Station Workflow
To become a true Papa’s Freezeria master, you must perfect the rhythm of the four key stations:
Order Station: Greet customers fast and double-check each ticket.
Build Station: Pour correct flavors and add mixables carefully.
Mix Station: Blend to exact smoothness—timing is everything.
Top Station: Add whipped cream, drizzles, and garnishes neatly for presentation points.
Tip: Focus on accuracy before speed. Perfect sundaes earn better tips, and those tips fund upgrades that make future shifts faster.
nice post and good job nice information thanks for sharing.
Post a Comment