The problem asks to find the largest set of vertices in a graph, such that no two vertices are adjacent.
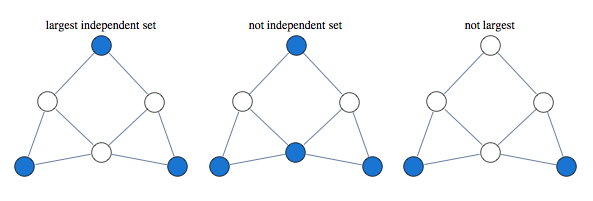
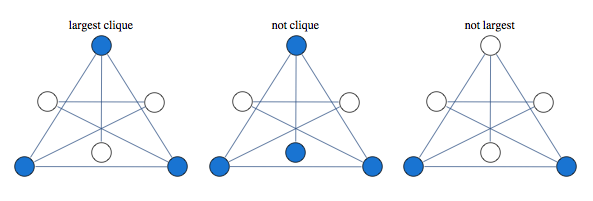
Finding largest independent set is equivalent to finding largest clique in graph's complement
A classical approach to solving this kind of problem is based on linear relaxation.
Take a variable for every vertex of the graph, let it be 1 if vertex is occupied and 0 if it is not occupied. We encode independence constraint by requiring that adjacent variables add up to 1. So we can consider the following graph and corresponding integer programming formulation:

$$\max x_1 + x_2 + x_3 + x_4 $$
such that
$$
\begin{array}{c}
x_1+x_2 \le 1 \\\\
x_2+x_3 \le 1 \\\\
x_3+x_4 \le 1 \\\\
x_4+x_1 \le 1 \\\\
x_i\ge 0 \ \ \forall i \\\\
x_i \in \text{Integers}\ \forall i
\end{array}
$$
Solving this integer linear integer program is equivalent to the original problem of maximum independent set, with 1 value indicating that node is in the set. To get a tractable LP programme we drop the last constraint.
If we solve LP without integer constraints and get integer valued result, the result is guaranteed to be correct. In this case we say that LP is tight, or LP is integral.
Curiously, solution of this kind of LP is guaranteed to take only values 0,1 and $\frac{1}{2}$. This is known as "half-integrality". Integer valued variables are guaranteed to be correct, and we need to use some other method to determine assignments to half-integer variables.
For instance below is a graph for which first three variables get 1/2 in the solution of the LP, while the rest of the vertices get integral values which are guaranteed to be correct

Here's what this LP approach gives us for a sampling of graphs

A natural question to ask is when this approach works. Its guaranteed to work for bipartite graphs, but it also seems to work for many non-bipartite graphs. None of the graphs above are bipartite.
Since independent set only allows one vertex per clique, we can improve our LP by saying that sum of variables over each clique has to below 1.
Consider the following graph that our original LP has a problem with:

Instead of having edge constraints, we formulate our LP with clique constraints as follows:
$$x_1+x_2+x_3\le 1$$
$$x_3+x_4+x_5\le 1$$
With these constraints, LP solver is able to find the integral solution

In this formulation, solution of LP is no longer half-integral. For the graph below we get a mixture of 1/3 and 2/3 in the solution.

Optimum of this LP is known as the "fractional chromatic number" and it is an upper bound both on the largest clique size and the largest independent set size. For the graph above, largest clique and independent set have sizes 9/3 and 12/3, whereas fractional chromatic number is 14/3.
This relaxation is tighter than previous, here are some graphs that previous LP relaxation had a problem with.

This LP is guaranteed to work for perfect graphs which is a larger class of graphs than bipartite graphs. Out of 853 connected graphs over 7 vertices, 44 are bipartite while 724 are perfect.
You can improve this LP further by adding more constraints. A form of LP constraints that generalizes previous two approaches is
$$\sum_{i\in C} x_i\le \alpha(C)$$
Where $C$ is some subgraph and $\alpha(C)$ is its independence number.
You extend previous relaxation by considering subgraphs other than cliques.
Lovasz describes the following constraint classes (p.13 of "Semidefinite programs and combinatorial optimization")
1. Odd hole constraints
2. Odd anti-hole constraints
3. Alpha-critical graph constraints.
Note that adding constraints for all maximal cliques can produce a LP with exponential number of constraints.
Notebook
Packages
176 comments:
Cool post.
So in a practical setting, if we wanted to solve large maximum independent set problems with this approach, we could imagine starting with the basic set of edge constraints, running the LP, checking to see if we have an integral solution, and if not, intelligently adding new constraints.
Do you have any ideas about good ways to choose which additional constraints to add?
(As you may know, this is essentially the problem addressed in the following paper, though the paper is about general MAP inference rather than MIS:
D. Sontag, T. Meltzer, A. Globerson, Y. Weiss, T. Jaakkola. Tightening LP Relaxations for MAP using Message Passing. Uncertainty in Artificial Intelligence (UAI) 24, July 2008.)
Look at, say, graph on (4, 5) position in the first big picture. It is not the only optimal LP solution, an off-the-shelf LP algorithm can assign 1/2 to the both nodes in the left column, and to the both nodes in the right column. So, should one use some technique that prefers integral solutions? Is it the common case when there are several optimums, and integral among them?
Roman - Good question, I actually don't know why integer solution was chosen in that case. There are quite a few cases like that, with non-unique maximum, yet the solver choosing an integer solution, perhaps it's a side effect of the simplex method
Danny - that sounds like a promising approach -- here you could see which regions of the graph produce non-integer solutions, add constraints of the last kind for those vertex sets, and rerun the LP solver
Concerning Roman's question I think it is possible to add random small epsilons (either positive or negative) to the right parts of constaints in LP relaxation. We will seem to loose the property of half-integrality but in such unlikely case when there are several solutions we will definitely converge to the integer one.
I think the reason of 1/2 solution is that the variable takes value 1 in some of the maximum independent sets and 0 in others. In easy cases of Independent-Set, e.g. on Erdos-Renyi random graphs with average connectivity smaller than 2.71828..., leaf-removal algorithm gives an optimal solution, then I guess LP will give a tight solution. In hard cases, when leaf-removal core exists, no efficient algorithm exists to solve the problem, and LP gives fraction solution.
In my example with the bowtie graph, there's no maximum independent set that contains middle node, yet it gets value 1/2
The possible sets of nonintegral values in optimal LP solutions are closed under intersection (Picard&Queyranne: On the integer-valued variables in the linear vertex packing problem, 1977, http://dx.doi.org/10.1007/BF01593772). Thus, there is a unique optimal LP solution with the minimum number of fractional values, and you can find it for example by trying to fix each variable to 1 and seeing if the objective changes.
On G(n, p)-graphs, for any p, with high probability all variables 1/2 is the only optimal LP solution (Pulleyblank: Minimum node covers and 2-bicritical graphs, 1979, http://dx.doi.org/10.1007/BF01588228).
For Roman's question, the 1/2-solutions proposed are not basic solutions since they are the convex combination of other solutions (in particular, the alternative integer solutions). So, as long as your LP algorithm returns basic solutions (for instance the simplex algorithm; interior point methods have approaches that force basic solutions but that is not required), you will not get the 1/2 solutions.
Jayati Tools Private Limited is a trusted company which is Manufacturer and Supplier of scaffolding equipment all over the world. We are manufactur the Scaffolding Accessories, composite die holder, scaffolding socket, Tuff Scaffolding Machine and all types of Scaffolding equipments. www.scaffoldingmachines.com
This is a awesome blog post.
I want a program for this.
Why does the LP relaxation work on perfect graphs?
Interesting stuff to read. Keep it up.
Machine Learning Solutions Provider
Learn online Digital marketing
Great post with nice information thanks for sharing
Nice Blog.!
Machine Learning Solutions Provider
Nice blog well said useful information thank you so much
Deep Learning Training in Hyderabad
Nice information thank you
Deep Learning Training in Hyderabad
Nice informative blog. Keep updating these types of informative updates regularly and also please visit our link
Machine Learning Training in Hyderabad
Crafsol is the best leading machine solution provider in Pune, India, USA, South Africa, Indonesia, UK, France and Germany.
Machine Learning Solutions Provider
Nice blog thank you for sharing this information
Machine Learning Training in Hyderabad
thank you for the information, may this blog information can useful to the people who are confuse. for more details visit us at
Deep Learning Training in Austin
In recent time one of the finest program for the writing is held upon in canada and there has lots of way to get known as a writer. http://www.ukraineoutsourcingrates.com/sql-development-ukraine-rates/ to see more about the wrting tips.
i was learned nice information about this topic.
Aws Online Training
PCB Design Training in Bangalore offered by myTectra. India's No.1 PCB Design Training Institute. Classroom, Online and Corporate training in PCB Design
pcb design training in bangalore
Really nice post.
myTectra offers corporate training services in Bangalore for range of courses on various domain including Information Technology, Digital Marketing and Business courses like Financial Accounting, Human Resource Management, Health and Safety, Soft Skill Development, Quality & Auditing, Food Safety & Hygiene. myTectra is one of the leading corporate training companies in bangalore offers training on more than 500+ courses
corporate training in bangalore
top 10 corporate training companies in india
along these we are going to help professionals and students to crack their interview with some interview questions and answers
bootstrap interview questions
dbms interview questions
Great Post,
https://bitaacademy.com/
IOT Training in Bangalore - Live Online & Classroom
IOT Training course observes iot as the platform for networking of different devices on the internet and their inter related communication.
Nice to see this article. Keep update with useful information.
Machine Learning Services
Cerita Dewasa Dan Sex Terlengkap & Terbaru
Cerita Dewasa
Tolong jelaskan saya gak ngerti maksudnya, Sedot WC Kediri
Useful post, thanks for sharing.
Spring Training in Chennai
Hibernate Training in Chennai
Struts Training in Chennai
RPA Training in Chennai
AngularJS Training in Chennai
AWS Training in Chennai
DevOps Training in Chennai
R Programming Training in Chennai
Meaning full post thanks
Best R programming training in chennai
Really useful information. Thank you so much for sharing.It will help everyone.
R Training Institute in Chennai | R Programming Training in Chennai
Thanks for sharing the informative blog. Web journal you’ve provided is so simple and reasonable, and mainly the substance of data is educational. You can also read more valuable and beneficial information on Janbask Training. I found it really helpful to broaden my knowledge in terms of Machine Learning.
Good post..Keep on sharing....
GCP Training
Google Cloud Platform Training
GCP Online Training
Google Cloud Platform Training In Hyderabad
This is one awesome blog article. .
Machine Learning Training in Gurgaon
Machine Learning Course in Gurgaon
Machine Learning Training institute in Gurgaon
This is the best site i ever seen. Thank you for the information and also don't forget to visit my site download pkv games
https://www.blogger.com/comment.g?blogID=10560800&postID=1041951345399867160&page=1&token=1561618037021
Good Post! Thank you so much for sharing this pretty post, it was so good to read and useful to improve my knowledge as updated one, keep blogging.
Artificial Intelligence Training
Data Science Training
thanks for sharing this information
best java training in chennai
best python training in chennai
best python training institute in omr
python training in omr
selenium training in chennai
selenium training in omr
selenium training in sholinganallur
java training in omr
Berita Bola Terkini | Piala Eropa 2020
This concept is a good way to enhance knowledge.thanks for sharing. please keep it up machine learning online course
It is very good and very informative. There is a useful information in it.Thanks for posting... Machine Learning Training In Hyderabad
Thanks for sharing such a great blog Keep posting..
Machine Learning Training in Delhi
dadu online uang asli permainan terbaik sepanjang masa.
Thanks for delivering a good stuff related to GCP, Explination is good, Nice Article.
GCP Online Training
Google Cloud Platform Training In Hyderabad
bola88
situs judi slot online
casino online indonesia
judi bola terpercaya
link alternatif sbobet
live casino indonesia
judi slot online
situs judi online
link bola88
dewa casino
Great post, thanks for sharing!
Hương Lâm với website Huonglam.vn chuyên cung cấp máy photocopy toshiba cũ và dòng máy máy photocopy ricoh cũ uy tín, giá rẻ nhất TP.HCM
This blog contains very important information on Machine learning. This information is very much useful.
More information on this topic is awaited.
machine learning
Thanks for sharing valuable information.
Docker Training in Hyderabad
Kubernetes Training in Hyderabad
Docker and Kubernetes Training
Docker and Kubernetes Online Training
This post is so interactive and informative.keep update more information...
German Classes in Chennai
German Classes in Bangalore
German Classes in Coimbatore
German Classes in Madurai
German Language Course in Hyderabad
German Language Course in Chennai
German language course in bangalore
German language course in coimbatore
Selenium Training in Bangalore
Software Testing Course in Bangalore
Thanks for sharing your valuable information and time.
Machine Learning Training in Delhi
Cara Meningkatkan Peluang Menang Judi Poker Online Indonesia
Judi poker online saat ini terbilang sebagai salah satu permainan judi online yang sangat terkenal di Indonesia. Bagi anda yang suka berselancar pada dunia maya maka dapat menemukan situs poker online dengan mudah. Bahkan saat ini judi online seperti permainan poker telah menjadi hal yang sangat mudah diakses kapan saja dan dimana saja. Dengan kata lain saat ini permainan judi sudah tidak lagi dibatasi oleh ruang dan waktu. Bagi anda yang gemar bermain taruhan judi online, coba untuk bermain judi poker online dan poker uang asli untuk meraih keuntungan yang jauh lebih besar.
agen bola
Poker online
Poker Uang Asli
Prediksi Bola
Jadwal Bola
Agen Bola
dominoqq
bandarqq
poker qq online
pkv games
Hello, o you know that the best way to boost your brain is
visiting or contacting us
https://weiiitrading.com/our-products/moonrock-carts/buy-empty-moonrock-clear-vape-cartridges-blue-carts-dr-zodiak-atomizers-with-flavor-box-packaging/
https://weiiitrading.com/our-products/heavy-hitters-carts/buy-wholesale-new-heavy-hitter-vape-cartridges-1-0ml-ceramic-coil-empty-tank-carts-510-thread-thick-oil-atomizer/
https://weiiitrading.com/our-products/juul-carts/buy-hot-empty-ceramic-pod-disassembled-cartridges-0-7ml-1-0ml-vape-pod-carts-for-vape-juul-vape-pen-start-kit-top-quality/
https://weiiitrading.com/our-products/mario-carts/buy-peaches-and-dream/
https://weiiitrading.com/our-products/heavy-hitters-carts/buy-bubba-kush-cartridge-2-2g/
https://weiiitrading.com/our-products/mario-carts/buy-thin-mint-cookies/
Pila Brass Knuckles Online for sale online,
where to buy Buy Pila Brass Knuckles Online
buy valley online cartridge
buy space candy online
buy cannabis syrup online
buy botox online
cannabis bread
uk chese
47 dank vapewhite fire og
buy moonrock
Email Us
Contact: +1 619-537-6734
How cool was that having a full Car diversion System best 6x9 speakers Through this I really makes the most of my ride each time uniquely while out and about with a few companions. So amazing!
Good Article & Informative. Thanks for Sharing.
python training in Hyderabad
Data science in Hyderabad
digital marketing institute
Aws online training
full stack developer course
great post ! helpful post
learn more about save water and life
Get more computer courses
best certification courses for java developers
java training institute in jaipur
java programming training classes
learn more about save water and life
Get more computer courses
best certification courses for java developers
java training institute in jaipur
java programming training classes
Startup Jobs, Off campus drive,
Startup News, IT Jobs, Engineering Jobs
TCS, Infosys, Microsoft, Google, Tech Mahindra, Capgemini, OYO, Ola,
Amazon, Flipkar, Jobs, Internship, Freshers job, Off
campus drive
Red Hat Certified Engineer is a professional who has expertise in handling the Red Hat Enterprise Linux System. The Certified Engineer takes care of various tasks such as setting kernel runtime parameters, handling various types of system logging and providing certain kinds of network operability.
Red Hat Certified Engineer
Thanks for sharing Great info...Nice post.
Machine Learning
Wow! Thanks for sharing this valuable blog with us. I Would like to share something useful with you regarding machine learning clinical trials. I hope this will give you some suggestions to work on your upcoming blogs.
Really great info and valuable blog.
Thank You
iis university
Best academic environment at university campus
best girls university in jaipur
Best girls college in Rajasthan
top 10 mba college in jaipur
Admission in university with hostel facility in Rajasthan
Situs IDN Poker88
Poker88 asia— Situs IDN Poker88 online terpercaya dan terbaik di Indonesia ialah www.imfbet.com. Agen resmi IDN Poker88 yang sudah banyak dikenal oleh para pemain judi online di Indonesia yang menyediakan berbagai macam-macam jenis permainan judi kartu online.
Anda dapat menikmati berbagai macam permainan kartu dari provider IDN Poker88 dalam situs ini. Pemain IDN Poker88 juga tersedia dalam HTML5 untuk smartphone android atau IOS yang telah disesuaikan dengan perangkat dari smartphone anda.
Game Slot “Lucky Lucky”
Judi slot— Jika anda ingin mencari game slot favorit anda untuk game slot online yang ‘sederhana sederhana’ maka kami mungkin memiliki apa yang anda cari di sini dalam bentuk game slot Lucky Lucky, sebuah permainan yang dikembangkan oleh Habanero Systems tanpa ada yang menghalangi fitur bonus,tetapi banyak cara.
nice info you are sharing thank you so much.
Aviation institute
Air Hostess institute
airport ground staff training institute
hospitality and travel management institute in Jaipur
Cabin Crew training institute
meraih keuntungan yang banyak di live game IDN. kalian bisa melihat panduan cara bermain game
- ROULETTE
- 12D
- 24D
- 24Dspin
- 3D Shio
- 5D Ball
- Baccarat
- Billiards
- Dice 6
- Dragon Tiger
- Fantan
- Gong Ball
- Head Tail
- Monopoly
- Race Ball
- Sicbo[Dice]
Semua bisa kalian pelajari di Cara Bermain Live Game IDN LIVE
Game Slot “Bomb Away”
Judi slot— Bombs Away adalah game slot dari Habanero yang berlangsung selama konflik bersenjata terbesar abad ke-20. Sebagai pemain, Anda akan bertanggung jawab untuk memastikan bahwa tentara mendapat dukungan yang dibutuhkan untuk memenangkan peperangan demi kebebasan dan menyelamatkan negara.
Game Slot “Wild Spells”
Kartu joker— Wild Spells adalah game slot yang memiliki 25-payline, Slot ini terinspirasi oleh kekuatan sihir penyihir dan ahli sihir yang perkasa, dan juga dibumbui dengan botol ramuan dan buku mantra. Simbol yang paling penting adalah Purple Cat, yang merupakan simbol Wild, dan Crystal Ball, yang merupakan singkatan dari simbol Scatter.
Game Texas poker88 IDN Terbaik
Poker88 asia— Untuk permainan Texas poker tentunya sudah tidak asing lagi bagi para pecinta judi poker online yang sering dimainkan di Indonesia, Texas poker ini sangatlah banyak peminat diseluruh dunia.
IDN Poker adalah salah satu penyedia permainan judi kartu online terbesar di Indonesia dan asia. Texas poker ini menggunakan kartu remi dan bisa dimainkan minimal 2 orang dan maksimal 8 orang dalam satu meja.
Cara Bermain Judi Bola Online Over/Under
Judi bola online— Dalam Kesempatan ini admin masih akan terus tidak akan pernah bosen memberikan tips atau cara bermain judi bola online yang sangat mengungtungkan untuk anda. Kali ini jenis taruah yang akan admin berika adalah Over/Under.
Cara yang sangat ampuh menebak jenis taruhan Over. Sebelum masuk ke inti dari masalah pembahasan kali ini, admin ingin mengajak anda sebelum nya yang mungkin belum memiliki user ID untuk bermain judi bola online. Imfbet adalah agen atau situs resmi yang menyediakan jasa pembuatan akun judi online seperti, Sportsbook, casino, Slot game, poker dan masih banyak yang lainnya.
Keuntungan Bermain di Server IDN Poker88asia
Poker88 asia— Halo, semua ! Bagi para pecinta judi poker online pasti sudah tidak asing lagi mendengar tentang beberapa server judi poker online terkenal di Indonesia saat ini. Di Indonesia memiliki beberapa server perjudian poker online, dalam artikel kali kami akan membahas tentang keuntungan dari situ Agent IDN Poker88.
Really nice and interesting post. I was looking for this kind of information and enjoyed reading this one.data science course
I really like reading through a post that can make people think. Also, many thanks for permitting me to comment!
Kumkum Bhagya
Apa Kelebihan S1288Poker ? Kenapa harus main di S1288Poker ?
• Bonus Deposit New Member 10% (Rp 5.000.000,-)
• Bonus Deposit Setiap Hari (Otomatis Masuk Setelah Deposit)
• Bonus Turnover Setiap Minggu (Selasa & Jum'at)
• Bonus Deposit Pulsa Tanpa Potongan (Telkomsel, XL & AXIS)
• Bonus Tanpa Deposit Hadir Setiap Bulan (S&K Berlaku)
Bank Online 24 Jam, Proses cepat, withdraw / tarik dana tidak pending, tidak basa basi, terpercaya dari tahun 2015.
• Daftar >> Freechip Gratis
s128cash
s1288poker
Watch Bigg Boss 14 Colors Tv Show HD Full Episodes Video By Voot, Free Download Bigg Boss 14 Complete All Episodes in High Quality.
Watch Bigg Boss 14 Voot Show Full Episodes Video By Colors Tv Online in HD, Indian Reality Show Bigg Boss 14 Download in full HD.
I just learn how to unblock someone on facebook from android forum
tp link admin login page
Watch Bigg Boss Season 14 All Episodes Online
Kasauti Zindagi Ki Watch Online Star Plus Full Episodes
Kiran Infertility Centre – Chennai’ is one of the best IVF Treatment in Chennai providing world-class treatment options like IVF, ICSI, Oocyte Donation, Surrogacy and Oocyte/Embryo freezing.ivf treatment in Chennai
I'm cheerful I found this blog! Every now and then, understudies need to psychologically the keys of beneficial artistic articles forming. Your information about this great post can turn into a reason for such individuals.
data science in malaysia
You will like it to enjoy our new app Camp Pinewood Mod Apk : which you could download and enjoy loose.
Excellent blog I visit this blog it's really awesome. The important thing is that in this blog content written clearly and understandable. The content of information is very informative.
DevOps Training in Chennai
DevOps Course in Chennai
Aivivu - đại lý vé máy bay, tham khảo
giá vé máy bay đi Mỹ khứ hồi
vé máy bay tết
vé máy bay đi Pháp khứ hồi
ve may bay di Anh gia re
đặt vé máy bay giá rẻ ở đâu
vé máy bay đi San Francisco giá rẻ 2020
vé máy bay đi Los Angeles giá rẻ 2020
combo đi phú quốc
combo đà nẵng 2 ngày 1 đêm
A dark shadow was cast on a certain peaceful little Quest Town Saga MOD APK
Download… Well, no, actually it was just a bunch of silly-looking monsters suddenly causing trouble. Anyway, someone’s got to teach them a lesson, and that’s you!
That's a beautiful post. I can't wait to utilize the resources you've shared with us. Do share more such informative posts. For more information regarding SEO Course and Digital Marketing Course Visit eMarket Education
I want to share with you all on how Dr Itua saves my life with his powerful Herbal medicines, I was diagnosed of Oral/Ovarian Cancer which i suffered from for 5 years with no positive treatment until when My son came to me in the hospital when i was laying down on my dying bed waiting for god to call out my name to join him in heaven.
My son was so excited that very day he came across Dr Itua on Blogspot, we decided to give him a try although we Americans are so scared to trust Africans but i really have no choice that time to choose life in between so we gave a try to Dr Itua Herbal medicines, god wiling he was a good man with a god gift. Dr Itua send us the herbal medicine it was three bottles. I take it for three weeks instructor and this herbal medicines heal me, cure my Oral/Ovarian Cancer completely I have been living for 9 months now with healthy life no more symptoms.
I'm sponsoring Dr Itua in LA Advert on Cancer patent seminar which my son will be participating too and other patent Dr Itua has cured from all kind of human disease, also if you are sick from disease like,Epilepsy,Breast Cancer,Prostate Cancer,Throat cancer,Thyroid Cancer,Uterine cancer,Fibroid,Angiopathy, Ataxia,Arthritis,Brain cancer,Hiv,. Vaginal cancer,Herpes,Colon-Rectal Cancer,Chronic Disease.Amyotrophic Lateral Scoliosis,Brain Tumor,Fibromyalgia,Fluoroquinolone Toxicity,Multiple myeloma,Tach Diseases,Leukemia,Liver cancer,
Esophageal cancer,Gallbladder cancer,,Bladder cancer,Gestational trophoblastic disease,Head and neck cancer,Hodgkin lymphoma
Intestinal cancer,Kidney cancer,Hpv,Lung cancer,Adrenal cancer.Bile duct cancer,Bone cancer,Melanoma,Mesothelioma,Neuroendocrine tumors
Non-Hodgkin lymphoma,Cervical Cancer,Oral cancer,Hepatitis,Skin cancer,Soft tissue sarcoma,Spinal cancer,Pancreatic Cancer, Stomach cancer
Testicular cancer,
Syndrome Fibrodysplasia Ossificans ProgresSclerosis,Alzheimer's disease,Chronic Diarrhea,Copd,Parkinson,Als,Adrenocortical carcinoma Infectious mononucleosis,Vulvar cancer,Ovarian cancer,,Sinus cancer, Here Is The Wonderful Healer Contact. Name_ Doctor Itua, Email Contact: drituaherbalcenter@gmail.com, Phone/WhatsApp: +2348149277967
Fantastic!! you are doing good job! I impressed. Many bodies are follow to you and try to some new.. After read your comments I feel; Its very interesting and every guys sahre with you own works. Great!!
vé máy bay đi đài loan giá bao nhiêu
vé máy bay từ tphcm đi đài bắc
vé máy bay đi cao hùng - đài loan
thoi gian bay tu tphcm den trung quoc
vé máy bay hà nội đi quảng châu
Berapa Harga dari Sedot WC Kediri?
I'm Serenity Autumn, currently living in Texas city, USA. I am a widow at the moment with Four kids and i was stuck in a financial situation in May 2019 and i needed to refinance and pay my bills. I tried seeking loans from various loan firms both private and corporate but never with success, and most banks declined my credit. But as God would have it, I was introduced to a woman of God a private loan lender who gave me a loan of 850,000.00 USD and today am a business owner and my kids are doing well at the moment, if you must contact any firm with reference to securing a loan without collateral , no credit check, no co signer with just 2% interest rate and better repayment plans and schedule, please contact Mrs Mr Bejamin Lee On Email 247officedept@gmail.com And Whats-App +1-989-394-3740. He doesn't know that am doing this but am so happy now and i decided to let people know more about him and also i want God to bless him more.
A whatsapp plus download Today we all are using many social apps like WhatsApp, Instagram, Facebook, and many more. WhatsApp.This is the best time to download the latest version of Yowhatsapp download and you’ll get the best version of WhatsApp on your devices.Fmwhatsapp new version download is the mod version of WhatsApp, FMWhatsApp Apk which offers you a Mod version.
really amazing blog it is .
Solar Power Plant In Jaipur
Solar Company in Jaipur
Solar Panel Manufacturers in jaipur
Solar Panel Company in Jaipur
Solar Power System in jaipur
AWS Training will provide you to learn about AWS, cloud services, computing, IAM, etc with realty. AWS Online Training also includes live sessions, live Projects.
AWS course
Our Business Analyst Training will provide you to learn about Business Analysis and its technical aspects with realty. Our Business Analyst Course includes live projects.
business analyst course
Thank you for sharing this amazing blog.
Thanks a lot.
I want to share infographic of applications of Machine Learning
You can also hire AI and Machine Learning Developers from Dark Bears.
" such good content "
cake shop near me
best cake shop near me
cake shop near me home delivery
cake shop in Mansarovar Jaipur
best cake shop in Mansarovar, Jaipur
cake bakery near me
Online Cake Delivery in Jaipur
cake online delivery in Jaipur
https://smartcakes.in/
Such a very useful information!Thanks for sharing this useful information with us. Really great effort.
artificial intelligence course in noida
Back Pain Treatment in Ahmedabad, Back Pain Treatment Near Me
https://livewellhospital.com/back-pain-treatment-in-ahmedabad/
Really great info you provided here.
Thank You
Machine Learning Training in jaipur
Artificial Intelligence Training in Jaipur
Sales force Training in Jaipur
Java Training in Jaipur
Android Training in Jaipur
gamelan togel
http://gamelantogel.com/
Aivivu - đại lý chuyên vé máy bay trong nước và quốc tế
vé máy bay đi Mỹ Vietnam Airline
mua vé máy bay thanh hóa đi sài gòn
vé máy bay hà nội giá rẻ
vé máy bay đi đà lạt
săn vé rẻ đi quy nhơn
giá taxi đi nội bài
combo nghỉ dưỡng đà lạt
Nice blog has been shared by you. before I read this blog I didn't have any knowledge about this but now I got some knowledge so keep on sharing such kind of interesting blogs.
UI UX Design Studio
Your blogs are amazing. Keep sharing. I love them Are you also searching for help with my assignment? we are the best solution for you. We are best known for delivering the best urgent assignment help.
This is quite a good blog.Are you also searching for Nursing Research Paper Help? we are the best solution for you. We are best known for delivering nursing writing services to students without having to break the bank.
Packers And Movers Delhi Get Shifting/Relocation
Quotation from ###Packers and Movers Delhi. Packers and Movers Delhi 100% Affordable and Reliable
***Household Shifting Services. Compare Transportation Charges and Save Time, ???Verified and Trusted Packers
and Movers in Delhi, Cheap and Safe Local, Domestic House Shifting @ Air Cargo Packers & Logistics
#PackersMoversDelhi Provides Packers and Movers Delhi, Movers And Packers Delhi, Local Shifting, Relocation,
Packing And Moving, Household Shifting, Office Shifting, Logistics and Transportation, Top Packers Movers, Best
Packers And Movers Delhi, Good Movers And Packers Delhi, Home Shifting, Household Shifting, Best Cheap Top
Movers And Packers Delhi, Moving and Packing Shifting Services Company.
As we all know that mobile apps are the biggest requirement of firms. Protocloud Academy is a leading Android Mobile app development institute in Jaipur. Our mentors will guide you to translate software requirements into workable programming code and maintain and develop programs with the help of live project training. They will also give you in-depth concepts knowledge in Android Application Development, JAVA language, and fine use of the Latest Android Studio and deployment on Android Devices like Smart Phone or Android Tablets. After completion of the training program, our experts will give advanced training to guide students with the latest technologies. We will provide the training certificates by approved technology partners to help students crack the interview and get their dream job.
https://www.protocloudtechnologies.com/android-app-development-course-in-jaipur/
Great info thanks for sharing Did you like the UK lottery result.so click here. Postcode
Learn power bi training from india's leading software training institute: Onlineitguru and get your dream job in your dream company. We provide Live Instructor-Led Online Classes with 100% job Assistance and 24 X 7 Online Support.
power bi online training | power bi online course
Contact Information:
USA: +1 7327039066
INDIA: +91 8885448788 , 9550102466
Email: info@onlineitguru.com
I read this post, Thanks for sharing this information.
Artificial intelligence training in pune
AI BASED AUTO RESOLUTION SKILLS FOR INSTANT EMPLOYEE SUPPORT & BETTER EMPLOYEE EXPERIENCE
AI service desk
The growth chart showing the list of manufacturing companies in Noida clearly shows that Noida is a preferred city for occupants due to its better infrastructure and improved law and order.
SalezShark CRM software is a well-known and indispensable system for any company. The CRM software Chennai is essential for the continuous growth of any company, whether it's at the micro- or macro level.
Awesome blog. I enjoyed reading your articles. This is truly a great read for me. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work!
data science training in malaysia
Awesome blog. I enjoyed reading your articles. This is truly a great read for me. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work!
data scientist training in malaysia
After reading your article I was amazed. I know that you explain it very well. And I hope that other readers will also experience how I feel after reading your article.
data scientist course in malaysia
Best Machine Learning Training in Bangalore
Machine Learning Training in Bangalore
Machine Learning Courses in Bangalore
Machine Learning Online Training in Bangalore
Machine Learning Online Courses in Bangalore
Machine Learning training institute in Bangalore
best machine learning course in india
best machine learning course online
Merely wanna remark that you have a very nice internet site, I enjoy the style and design it really stands out. We can have a hyperlink trade contract among us!
토토
바카라사이트
파워볼
카지노사이트
Thanks a lot for sharing this with all people you really realize what you’re talking approximately! Bookmarked. Kindly also visit my web site!
스포츠토토
토토
안전놀이터
토토사이트
I just like the valuable information you supply in your articles. I’ll bookmark your weblog and take a look at once more right here regularly.
사설토토
카지노
파워볼사이트
바카라사이트
looking to Buy 2-FDCK Online from a leading supplier? onlineresearchchemlab.com is the best research chemicals store where you can buy
For More Info
Email: info@onlineresearchchemlab.com / onlineresearchchemlab@gmail.com
Wickr: locallegit
whatsapp: +1662-403-4557
Skype: williamjune1
Thanks for the great info. Awesome Post.
Kickcharm
Techycharm
Machine Learning Training in Gurgaon
JuliasNetwork
Situs Slot Tergacor No.1 Indonesia
You really make it look so natural with your exhibition however I see this issue as really something which I figure I could never understand. It appears to be excessively entangled and incredibly expansive for me.
Fantastic work! This really can be the kind of data which needs to really be shared round the internet. Shame on Google for perhaps not placement this specific informative article much higher! 릴게임
Machine Learning Training Institute in Noida
Machine Learning Course in Noida
Digital Marketing Institute in KPHB Emblix Academy – Digital marketing institute in KPHB, we address all major and minor aspects required for any student’s advancement in digital marketing. Clutch USA named our Digital Marketing Institute the best SEO firm. The future of digital marketing is promising and full of possibilities.
As a result, skilled digital marketers who can keep up with the rising demand are in high order.
In the Emblix Academy Digital marketing institute in KPHB, you will learn about all the major and minor modules of digital marketing, from Search engine marketing to Social Media Marketing and almost all Tools used for Digital Marketing.
We take pride in having onboard the most qualified and experienced domain experts with us. We have been successfully offering excellent Do my Law homework help services to students securing them only the best academic grades.
Thanks for sharing this wonderful article. I thought it was great. Your post is very educational. Moreover, your blog is very appealing.
customizefurniture.com!
Some pcb design training in bangalore of our popular courses include training, soft skills training, leadership development, project management,Change Management etc.
Nice blog article, thanks for sharing
msbi training in hyderabad
Webronix provides web development and social media services help businesses drive engagement and increase their visibility online. We leverage the latest technologies and trends to create custom digital solutions tailored to our client's needs. We strive to deliver high-quality results that exceed our clients' expectations.
That's a great article!
Good job.. Awesome blog post, I really appreciate if you continue this in future
Hii
Thank you for the informative article. You've shared a great blog. Before reading it, I lacked knowledge on this topic, but now I've gained some insights. Please continue sharing such interesting and informative blogs. Thank you Here is sharing some RPA Certification with UiPath Training information may be its helpful to you.
RPA Certification with UiPath
I'm glad to report that reading the post was interesting. Your article provided new information to me. You are performing admirably.
Testing Tools Training in JNTU
Thanks for sharing this wonderful article. I thought it was great. Your post is very educational. Moreover, your blog is very appealing.
java training in hyderabad
thank you for sharing this information
full stack courses
Linear programming (LP) is a mathematical technique used for optimization, where the goal is to find the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. It is widely used in various fields such as economics, business, engineering, and military applications.
Deep Learning Projects for Final Year Students
Image Processing Projects For Final Year Students
best kratom capsules
red borneo side effects
Growing Kratom
This is such a helpful guide! Using a Belgium virtual phone number via PVApins for Kakao account login is a game-changer. It’s great for protecting privacy and accessing all features without sharing personal info. Thanks for breaking it down so clearly!
Visit us:- https://pvapins.com/?/EN
I appreciate you sharing such great information.
Your website is really awesome.
The level of detail on your blog is impressive.
A highly readable article that presents a lot of helpful information.
This is such a great way to create a Hotmail account without using your personal phone number! 🌟 Using a Cambodia virtual number via PVApins makes the process super secure and private. 🔐 I love how easy it is to sign up without worrying about exposing my personal details. Definitely going to try this for my next account registration.
Visit us:- https://pvapins.com/?/EN
I just bookmarked your site. Very helpful for learning.
super kontol super kontol super kontol super kontol
Hm
Great article! I found your explanation of using linear programming for the Maximum Independent Set problem really insightful—especially how you broke down the constraints and objective function. It's fascinating to see how optimization techniques can be applied to solve complex graph theory problems.
As someone currently exploring different areas of applied computer science, including algorithm design and software quality assurance, I’ve also been looking into Hyderabad software testing certification Training programs to broaden my skill set. It’s amazing how these foundational topics intersect in real-world applications. Looking forward to more posts like this!
Great post! Your explanation of using linear programming to solve the Maximum Independent Set problem was clear and insightful. It’s fascinating how mathematical optimization can be applied to such complex graph theory challenges. This kind of problem-solving approach is also highly relevant in fields like software testing, where optimization and efficient resource allocation matter a lot. For anyone interested in bridging theory with real-world application, especially in quality assurance and test automation, I highly recommend checking out this Software testing training in Hyderabad that covers both foundational skills and industry-relevant tools.
Really insightful post! It’s fascinating how linear programming techniques can be applied to such complex graph problems like the Maximum Independent Set. The mathematical breakdown and real-world relevance made it a great read. For those of us working in fields like test automation and software quality, understanding optimization concepts like this can actually help in designing more efficient systems.
By the way, if anyone’s exploring ways to level up their automation skills, I recently came across a solid Selenium Certification Training Hyderabad that blends theory with hands-on practice—definitely worth checking out for QA professionals!
Such helpful information! I’ll definitely refer back to this when writing on similar topics. Thank You
Great post! AWS DevOps is a game-changer for automating workflows and improving deployment efficiency. For those who want to learn it from scratch to advanced level, I highly recommend the AWS DevOps Training in Hyderabad by Version IT. Their real-time project approach makes learning faster and more effective.
Solar Battery Storage for Homes: How It Works & Benefits
https://solskenenergy.com/solar-battery-storage-for-homes-how-it-works-benefits/
Solar Battery Storage for Homes: How It Works & Benefits
Thanks For Such a Valuable Information . It is Very Useful Information Who Aspiring For Python Full Stack Training . Our Version IT Will Basic to Advance Level Training Join Now!
This blog on “Linear Programming for Maximum Independent Set” provides an insightful explanation of how optimization techniques intersect with machine learning and graph theory. The way it connects LP formulations with practical applications in data science, clustering, and network analysis is impressive. For anyone pursuing online IT courses with certification , especially in AI or optimization, this post offers valuable conceptual clarity and practical depth.
I was diagnosed with Parkinson’s disease four years ago. After traditional medications stopped working, I tried a herbal treatment from NaturePath Herbal Clinic Within months, my tremors eased, balance improved, and I regained my energy. It’s been life-changing I feel like myself again. If you or a loved one has Parkinson’s, I recommend checking out their natural approach at [www.naturepathherbalclinic.com]. info@naturepathherbalclinic.com
it is very good post
plastic surgery cost in india
I really love your site.
Great post! Your explanation of how Linear Programming can be applied to the Maximum Independent Set problem is both insightful and practical. I really appreciate how you broke down the constraints and objective function—it makes the concept much easier to grasp. The connection between combinatorial optimization and LP relaxation is especially fascinating. Looking forward to more articles diving deeper into optimization techniques!
online IT courses with certification
This is a very interesting take on solving the Maximum Independent Set problem using Linear Programming. The way you highlighted the role of LP relaxation and how it helps approximate solutions for such NP-hard problems was really helpful. It’s great to see complex mathematical concepts explained in such a clear and structured way. Thanks for sharing—looking forward to more optimization-focused content!
online IT courses with certification
Very impressive post. Thanks for sharing.
click here for more information
"Join our power bi online training to master interactive dashboards, reports, and data visualization techniques from anywhere."
Great Information
DevOps Training institute in Ameerpet
Nice post
Devops Training in Ameerpet
Nice Explanation
Devops Institute in Ameerpet
Post a Comment