Here's a Mathematica notebook using Manipulate functionality to let you visualize the shrinkage that happens with different matrices, assuming J(w)'s Hessian is the identity matrix. Drag the locators to modify eigenvectors of B.
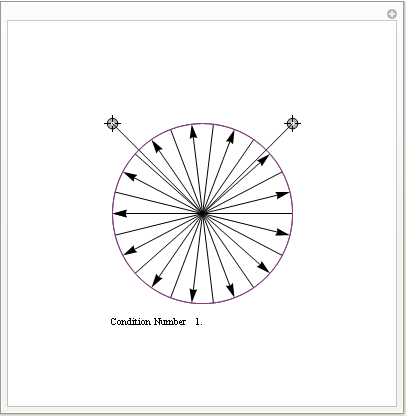
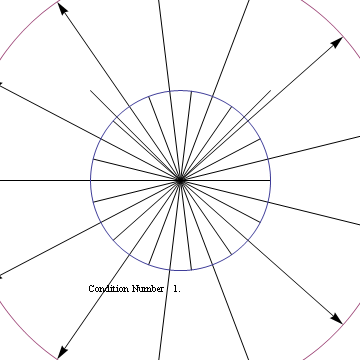
One thing to note is that if B is badly conditioned, strange things happen, for instance for some values of w*, they may get pushed away from zero. For negative-definite or indefinite matrices B you may get all w*'s getting shrunk away from zero, or they may get flipped across origin, where w* is argmax_w J(w)
Positive Definite
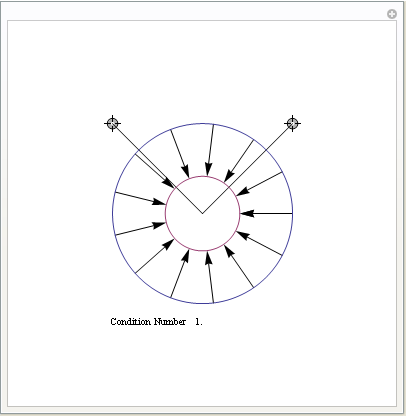
Indefinite
Negative Definite
2 comments:
Excellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
Assignment Writing Ace gives you an opportunity to get the expert assignment writing services . Their team of proficient assignment writers gives you the best results so that you can enhance and maintain the grades throughout the semester. They always assure plagiarism-free results and timely delivery of the assignment. Feel free to get the writing services for each type of academic assignments.
Post a Comment