Curse of Dimensionality and intuition

There are some counter-intuitive things happening as dimension increases.

For instance consider unit sphere (radius 1)



If you go from 2 dimensions to 3 dimensions, the volume increases (Pi to 4/3 pi). Similar increase happens when you go to 3,4,5 dimensions. But then the volume starts to decrease. Eventually it decreases all the way to 0.



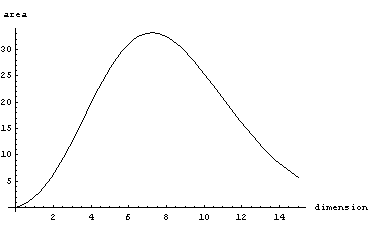
Now consider a cube of width 1. As dimension increases, the volume stays the same. But the length of the main diagonal grows as sqrt(dimension). So the corners become situated further and further away from the center, and eventually almost all the mass is concentrated in the corners (meaning outside of the inscribed sphere)

Here's a plot of the fraction of the mass concentrated in the corners as a function of dimension



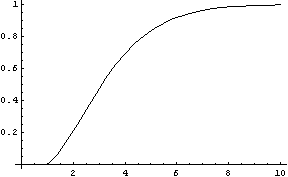
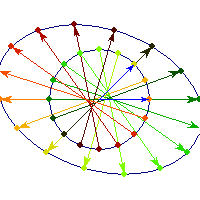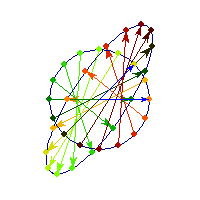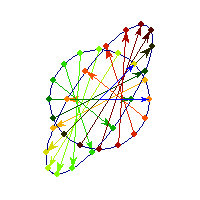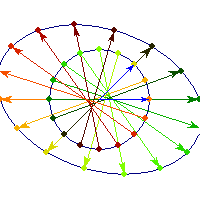
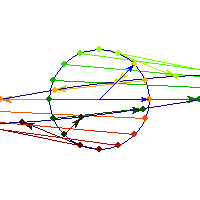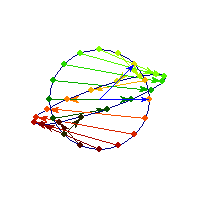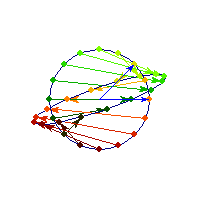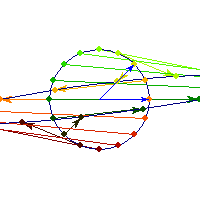
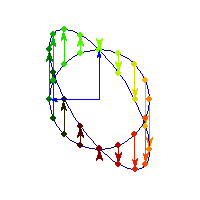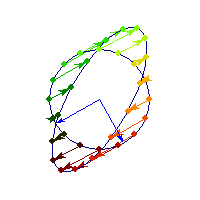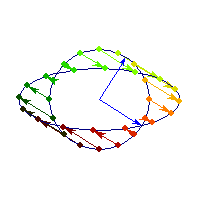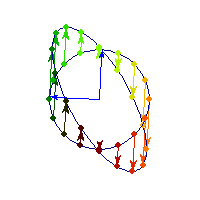
For a 7 dimensional cube, about 96% of the mass is concentrated in one of it's 128 "corners", so if we had 7 dimensional vision, we might see that cube like this



Finally consider what happens with a d-dimensional standard normal (unit covariance matrix, centered at 0). If we plot probability mass contained around a thin shell of radius r as a function r we get the following graphs (d=1,d=4,d=16)

The mean of this distribution is



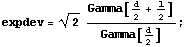
which can be approximated as sqrt(d)

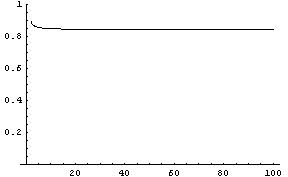
Furthermore you can derive that variance of this distribution converges to 1/2 (see notebook). Applying Chebyshev's inequality, we get that for any dimension, at least 0.75 of the mass is contained in the shell of thickness 1 centered at about sqrt(d). In numerical integration this seems to converge to a slightly higher number, for instance for 10^6 dimensions, it's about 0.84



Here's the Mathematica notebook with some derivations (web version)

Positive-definite/negative-definite

Concepts of positive definite matrices and positive definite operators often come up in Machine Learning, here are some movies I made to visualize linear transformations corresponding to some common types of matrices:

Symmetric and positive definite







Symmetric positive definite matrices can be thought of matrices that stretch or shrink the circle along the eigenvectors (marked in blue).

The angle between x and Ax is always less than Pi/2, so x'Ax>0 forall x.

Symmetric and negative definite


You can see in addition to stretching, every vector is flipped across the origin. So the angle is always between Pi/2 and Pi, hence x'Ax<0>0 and for others x'Ax


Symmetric and indefinite



Vectors are flipped across one axis only, so sometimes the angle is more than Pi/2 and sometimes it's less. A quadratic form corresponding to such matrix will have a saddle point (you can see this because x'Ax will be positive along some directions, and negative along others)

Positive definite but not symmetric

Rotation by less than Pi/2 and positive skew are positive definite operations, even though they are not symmetric or diagonalizable.











You can see in the first case there's only one vector (0,1) that does't change direction after action by A, so there's only 1 eigenvector, hence the matrix is not diagonalizable. In the second case, every vector changes after action by A so there are no (real) eigenvectors, and matrix is again not diagonalizable.