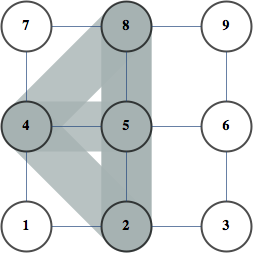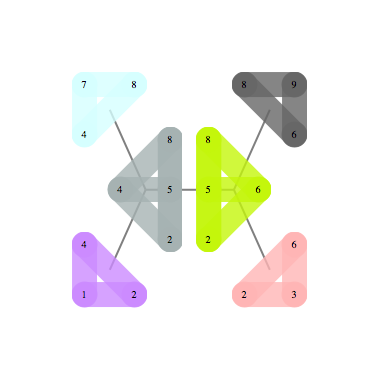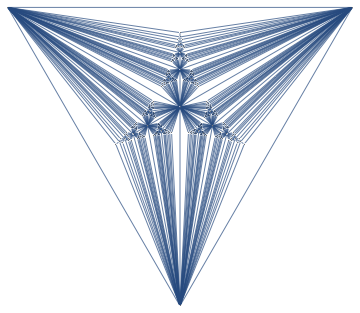
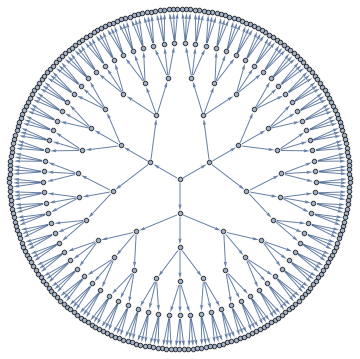
A Junction Tree provides an efficient data structure to do exact probabilistic inference. In the context of traditional graph algorithms, it is known as the "Tree Decomposition". The amount of structure apparent from the junction tree shows that problems structured as Apollonian Networks have very low computational complexity.
The same junction tree structure can also be used to efficiently compute chromatic polynomials, find cliques, count self-avoiding walks, and the reason for this universality is that it essentially captures separation structure of the graph -- it is a representation of a complete set of vertex separators. In the Junction Tree above you can see 121 non-leaf nodes that separate the graph into 3 parts. Each node corresponds to a set of 4 vertices. There are also 363 edges, each corresponds to a set of 3 vertices that separates the graph into 2 parts. The fact that the graph can be recursively partitioned using small separators implies an efficient recursion scheme for problems on this graph.
I put together a Mathematica package to build Junction Trees like above using MinFill, MinCut and a few other heuristics. Some experimenting showed MinFill with Vertex Eccentricity for choosing between vertices with equal fill to work the best for general graphs, whereas MinCut worked the best for planar graphs.