For instance, Globerson/Jaakkola do approximate counting by decomposing graph into planar graphs. In each part, the problem reduces to perfect matchings which can be solved efficiently on planar graph. Bouchet/Jordan decompose counting bipartite perfect matchings into much easier problems that count matchings perfect on "one side" of the graph. Sontag/Jaakola solve subproblems on star-shaped subgraphs of original graph, the symmetry of star graph enabling a very fast solution to each subproblem.
I recently came across graph class database which gives information on thousands of graph classes. It shows dozens (hundreds?) distinct tractable classes for exact maximum independent set, and most of them seem to have unbounded tree width. I haven't heard of most of those classes and would be curious to know how many distinctly interesting algorithms they correspond to
Here are a few computationally nice structures I've seen employed in Machine Learning and Vision literature
Upper-bounded tree width
Everything is easy via tree decomposition
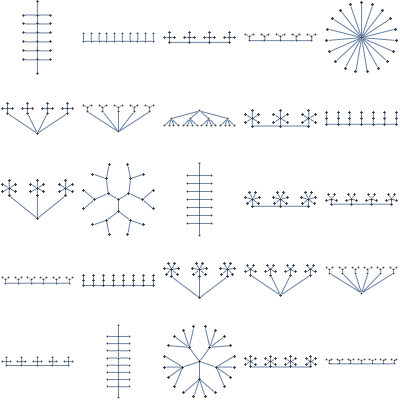
Lower-bounded girth
Almost everything is easy via loopy belief propagation
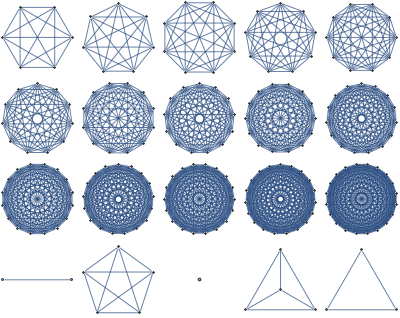
Planar
Easy minimization of submodular functions. Easy counting of certain structures by reduction to perfect matchings.
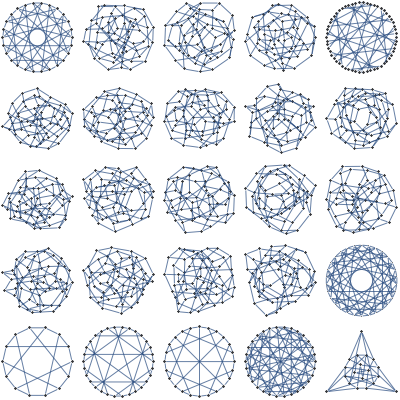
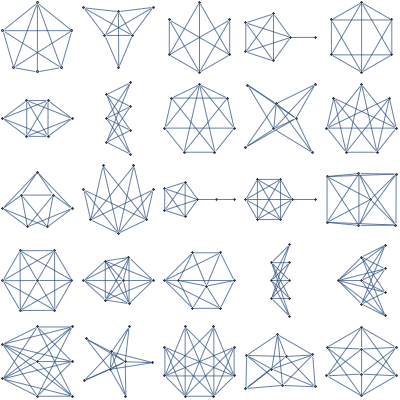
Complete
Easy counting of unweighted local structures
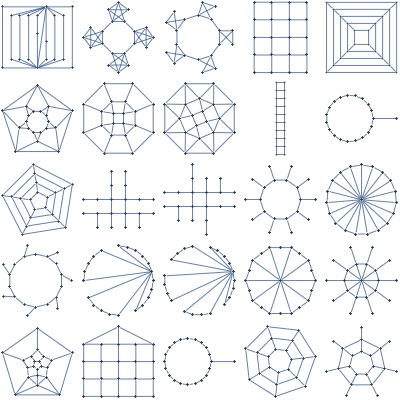
Perfect
Easy MAP inference with NAND potentials
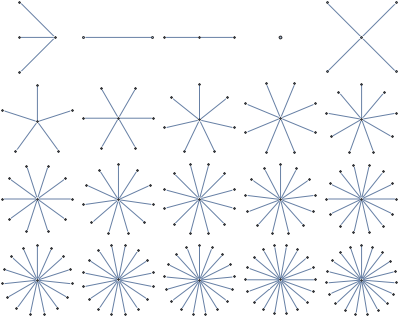
Star
Very efficient updates for MAP inference
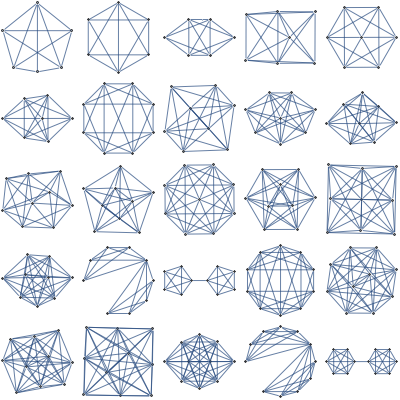
Claw-free
A generalization of line graphs. Easy maximum independent set, and counting by reduction to matchings
Any other useful classes I missed?
Mathematica notebook
10 comments:
Sorry for not giving anything insightful but all I can say - Very pretty! :)
Yeah, Mathematica has a pretty nice collection of graph embeddings, I'd guess Eric Weisstein had something to do with it
Thanks for sharing the graph class database! I just took an algorithms course, and if I would have known about that database, I would have been much better of.
Seems like there are a lot of graph classes... I'd be curious if some graph classes reduce to other graph classes. Then I'd also be curious whether there exist primitive graph classes that can universally construct all graph classes. And if we can find these primitive graphs, then we will have a better idea as to which algorithms can count those particular graphs.
This is the same idea as you've suggested above (breaking down graphs)... I'm just looking at it from the bottom-up.
Minor-exclusion characterizes classes described by contraction-closed properties. I would guess it's the only universal kind of description for those graph classes. But you could come up with new graph glasses that have a different characterization (concatenation closed properties?).
More generally, you have to answer "What is a graph class, and why do I care?" There's unlimited number of ways to group graphs into classes. The graph database I gave focuses on minor-exclusion categorization, and this kind of grouping seems useful if you are interested in complexity of problems like independent set. Alternative way to group graphs is by symmetry, ie, order of graph's automorphism group. I imagine there are some tasks that are easier to solve on highly symmetric graphs.
True. Graphs (like most data structures) can be described as groups.
After more investigation, I found that the Robertson–Seymour theorem proves that graphs that are closed under their graph minors have a well-quasi-ordering such that you can find forbidden minors that can act as the primitives of the graphs.
Now that we have conditions defined under the group (needs to be built upon forbidden minors), I guess the question is what operations can we apply to the graph such that they remain within the group after the transformation.
I'm not up to stuff in this area of study, so I'm not going to suggest anything, but it sounds really interesting. For example, I'm curious what matrix operations would be valid on the graph if we transformed the forbidden minors into matrices. Would they stay in the group if we did a matrix multiplication?
Excellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
Hi.., excellent websites you possess at this time there.
best machine learning course online
Machine Learning Online Training In Hyderabad
What’s up it’s me, I am also visiting this website daily, this website is really pleasant and the viewers are really sharing good thoughts
Thanks for the interesting article about technology.
Post a Comment