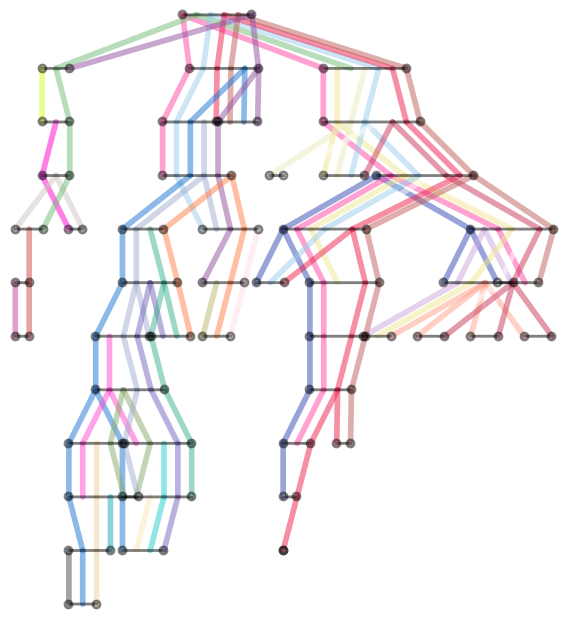
In order to do exact probabilistic inference on real life network efficiently, one must find a good Tree Decomposition of the network. This process is known as the Junction Tree algorithm. It's a bit hard to visualize the result, but while browsing tree decomposition
graph pages on Wikipedia, I got an idea. Instead of bags with variables, we plot it as a collection of colored strips where each strip corresponds to a variable and Running Intersection property guarantees there will be no breaks.
Here's the result for the width-7 tree decomposition of the moralized
Barley network
 Mathematica source
Mathematica source

6 comments:
Very cool. I like it.
Thanks! I do wonder when the tree decomposition captures the difficulty of exact solution...what kind of problems can your combinatorial MAP approach solve?
THANKS FOR THE INFORMATION...
<a href="http://www.chloros.in/digital-marketing-internship.htmlhttp://www.chloros.in/digital-marketing-internship.html>Digital Marketing Internship Program in Bangalore</a>
Excellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
Interesting exploration of tree decompositions! Understanding the graph structure is crucial for various algorithms. Has anyone considered using a tree decomposition to optimize solving puzzles like in Infinite Craft? Building from Tree + House = Treehouse, then Treehouse + Dream = Utopia, maybe this logic can be mirrored in graph traversal for faster solutions! More examples and practical applications would be great.
Post a Comment