Traditionally people do it by minimizing log-loss on data, which is equivalent to maximum likelihood estimation, but that has the property of recovering the conditional distribution exactly with enough data/modelling freedom. We don't care about exact probabilities, so in some sense it's doing too much work.
Additionally, log-loss minimization may sacrifice classification accuracy if it allows it to model probabilities better.
Here's an example, consider predicting binary y from real valued x. The 4 points give the possible 4 possible x values and their true probabilities. If you model p(y=1|x) as 1/(1+Exp(f_n(x))) where f_n is any n'th degree polynomial.
Take n=2, then minimizing log loss and thresholding on 1/2 produces Bayes-optimal classifier
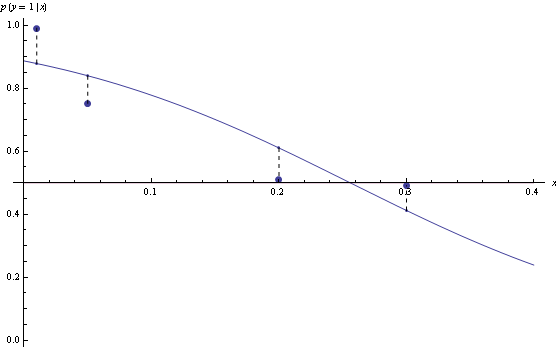
However, for n=3, the model that minimizes log loss will have suboptimal decision rules for half the data.
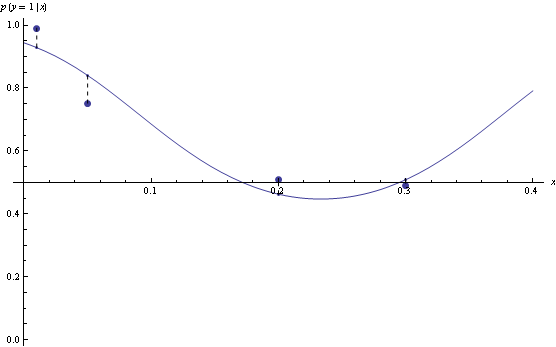
Hinge loss is less sensitive to exact probabilities. In particular, minimizer of hinge loss over probability densities will be a function that returns returns 1 over the region where true p(y=1|x) is greater than 0.5, and 0 otherwise. If we are fitting functions of the form above, then once hinge-loss minimizer attains the minimum, adding extra degrees of freedom will never increase approximation error.
Here's example suggested by Olivier Bousquet, suppose your decision boundaries are simple, but the actual probabilities are complicated, how well will hinge loss vs log loss do? Consider the following conditional density
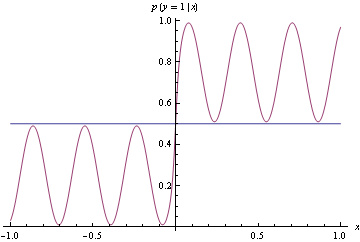
Now use the conditional density functions of the same form as before, find minimizers of both log-loss and hinge loss. Hinge-loss minimization always produces Bayes optimal model for all n>1
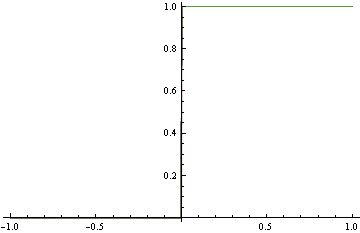
When minimizing log-loss, the approximation error starts to increase as the fitter tries to match the exact oscillations in the true probability density function, and ends up overshooting.
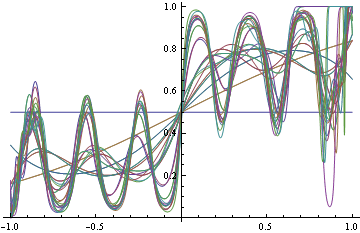
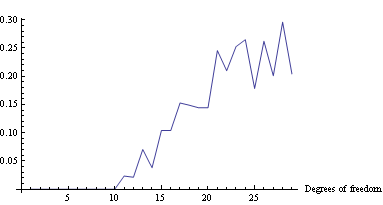
Here's the plot of the area on which log loss minimizer produces suboptimal decision rule
Mathematica notebook (web version)
12 comments:
Thanks
Great thanks for sharing about Machine learning. This post will be helpful for the readers who are searching for this type of information. Keep it up
Best Machine Learning institute in Chennai | machine learning with python course in chennai | best training institute for machine learning
Excellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
Great Article
IEEE final year projects on machine learning
JavaScript Training in Chennai
Final Year Project Centers in Chennai
JavaScript Training in Chennai
Đặt vé tại Aivivu, tham khảo
ve may bay di my gia re
thông tin chuyến bay từ mỹ về việt nam
từ canada về việt nam quá cảnh ở đâu
ve may bay vietnam airline tu han quoc ve viet nam
Thanks for machine learning project in your blog post...Its very useful for all students and learned more about in your blog post...We provideRFID project centers in chennai and research project centers in chennai projects titles with full source code at free of cost..
Thanks for your blog post. Its very useful and learned more in your articles .We provide projects for final year students in chennai. One of the best college project centers in chennai with quality projects at minimal cost.
First time reading this blog, thanks for sharing.
I find maximizing likelihood through minimum loss a compelling approach for fitting distributions.
Keep doing this in future. I will support you.
Your article is valuable for me and for others.
Post a Comment