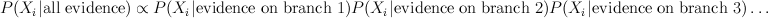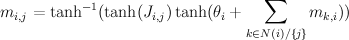Maximum entropy principle is the idea that we should should pick a distribution maximizing entropy subject to certain constraints. Many known distributions come out in this way, such as Gamma, Poisson, Normal, Beta, Exponential, Geometric, Cauchy, log-normal, and
others. In fact, there's a close connection between maxent distributions and exponential families -- Darmois-Koopman-Pitman theorem promises that all positive distributions with finite sufficient statistics correspond to exponential families. Recall that exponential families are families that are log-linear in the space of parameters, so in a sense, exponential families are analogous to vector spaces -- whereas vector space is closed under addition, exponential family is closed under multiplication.
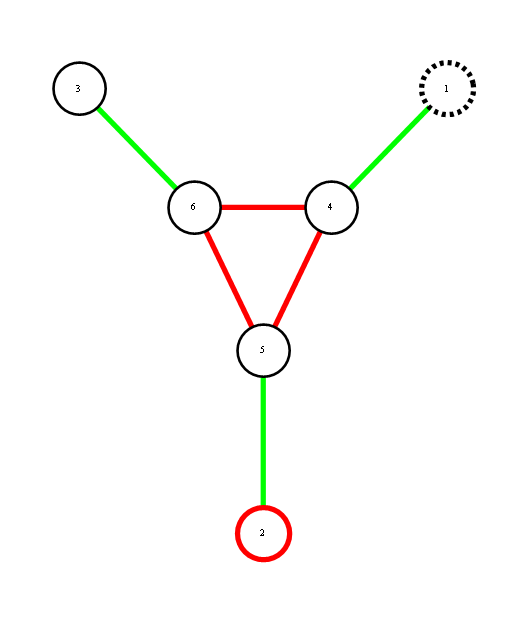
After you pick the form of your constraints, the maxent distribution is determined by the value of the constraints. So in this sense, constraint values serve as sufficient statistics, hence by DKP theorem, result must lie in the exponential family determined by form of the constraints.
You can use Lagrange multipliers (see my previous
post) to maximize entropy subject to moment constraints. This works to get Normal distribution and Exponential, but if you introduce skewness constraints you get distribution of the form exp(ax+bx^2+cx^3)/Z, which fails to normalize unless c=0, so what went wrong?
This is due to a technical point which doesn't matter for deriving most distributions -- correspondence between maxent and exponential family distributions only holds for distributions that are strictly positive. Also, entropy maximization subject to moment constraints is valid only if non-negativity constraints are inactive. In certain cases, like this one, you must also include nonnegativity constraints, and then the solution fails to have a nice closed form.
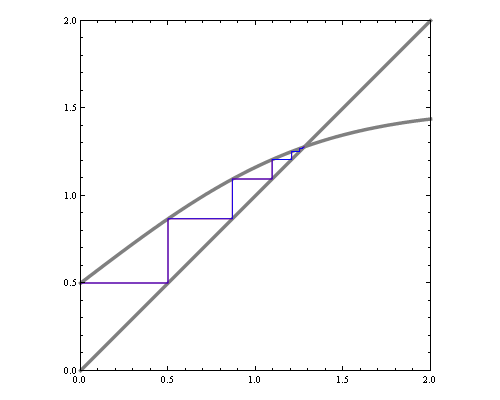
Suppose we maximize entropy in a distribution with 6 bins in the interval [-1,1] with constraints that mean=0, variance=0.3 and skewness=0. In addition to normalization constraint, this leaves a 2 dimensional space of valid distributions, and we can plot the space of valid (nonnegative) distributions, along with their entropy.
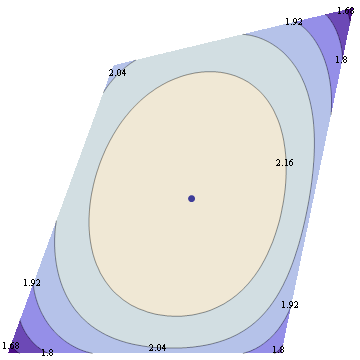
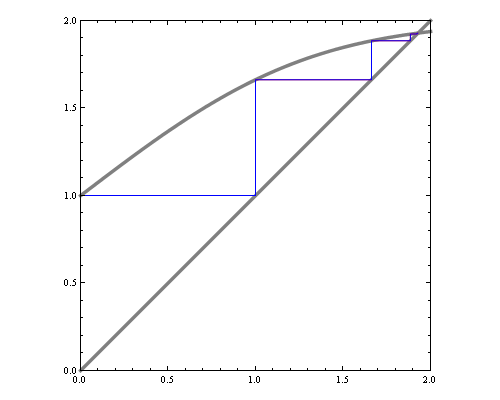
Now suppose we change skewness constraint to be 0.15 The new plot is below.
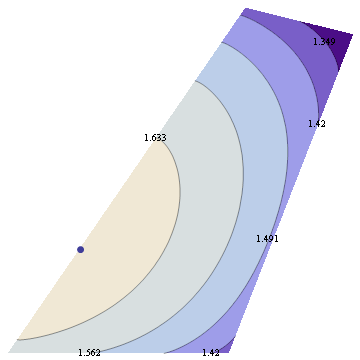
You can see that the maximum entropy solution lies right on the edge of the space of valid distributions, hence the nonnegativity constraint must be active at this point.
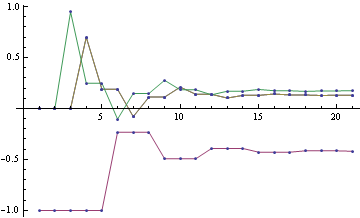
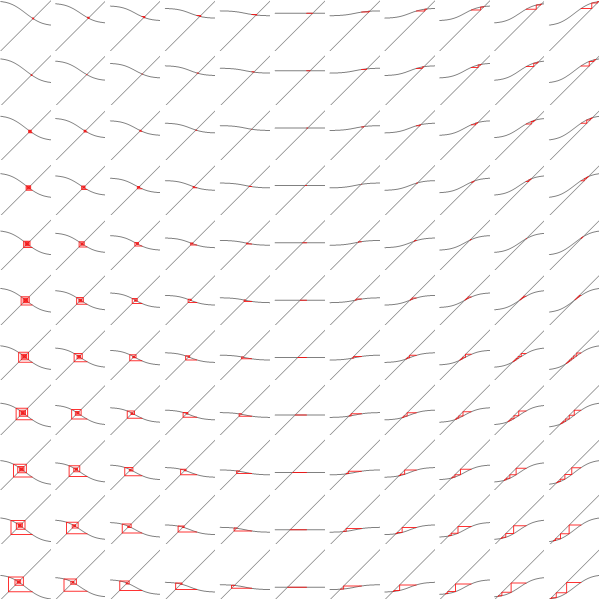
To get a sense what the maxent solution might look like, we can discretize the distribution, and do constrained optimization to find a solution. Below is the solution for 20 bins, variance=0.4 and skewness=0.23
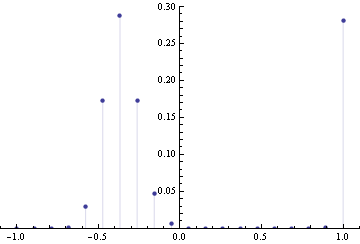
I tried various values of positive skewness, and that seems to be a general form -- distribution is 0 for positive x's except for a single spike at largest allowable x, for negative x's there's a Gaussian-like hump.
References:
-- Mathematica
notebook, web
version-- Justification of MaxEnt from statistical point of view by
Tishby/Tichochinsky
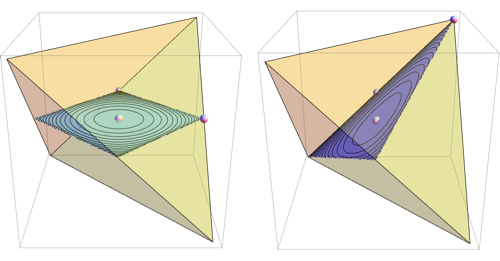







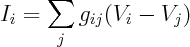
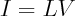
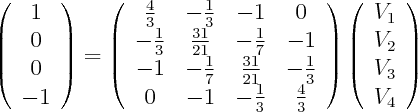
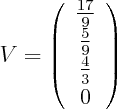
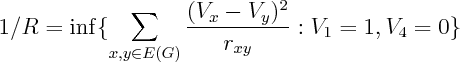 Corollary 5,
Corollary 5,