For instance consider unit sphere (radius 1)

If you go from 2 dimensions to 3 dimensions, the volume increases (Pi to 4/3 pi). Similar increase happens when you go to 3,4,5 dimensions. But then the volume starts to decrease. Eventually it decreases all the way to 0.
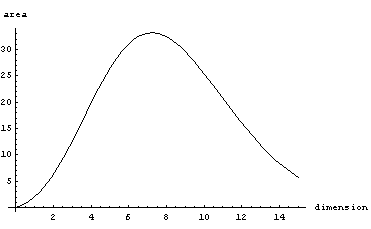
Now consider a cube of width 1. As dimension increases, the volume stays the same. But the length of the main diagonal grows as sqrt(dimension). So the corners become situated further and further away from the center, and eventually almost all the mass is concentrated in the corners (meaning outside of the inscribed sphere)
Here's a plot of the fraction of the mass concentrated in the corners as a function of dimension
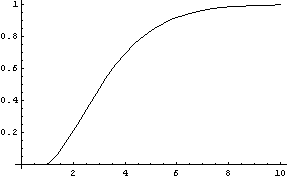
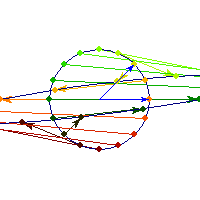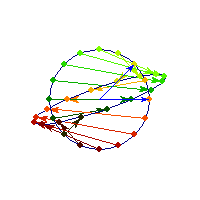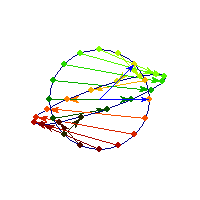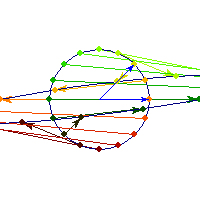
For a 7 dimensional cube, about 96% of the mass is concentrated in one of it's 128 "corners", so if we had 7 dimensional vision, we might see that cube like this

Finally consider what happens with a d-dimensional standard normal (unit covariance matrix, centered at 0). If we plot probability mass contained around a thin shell of radius r as a function r we get the following graphs (d=1,d=4,d=16)
The mean of this distribution is
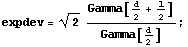
which can be approximated as sqrt(d)
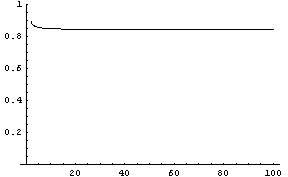
Furthermore you can derive that variance of this distribution converges to 1/2 (see notebook). Applying Chebyshev's inequality, we get that for any dimension, at least 0.75 of the mass is contained in the shell of thickness 1 centered at about sqrt(d). In numerical integration this seems to converge to a slightly higher number, for instance for 10^6 dimensions, it's about 0.84
Here's the Mathematica notebook with some derivations (web version)

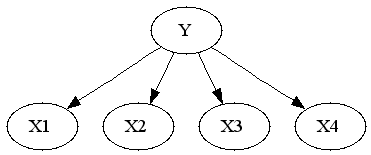
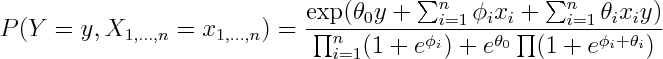
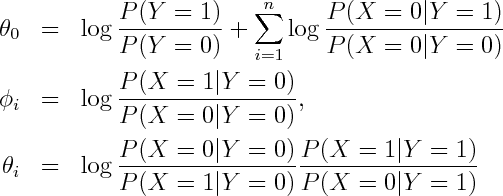
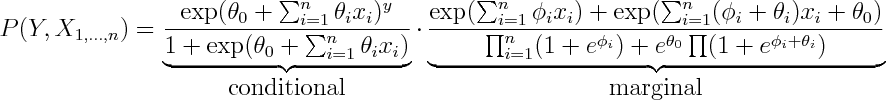
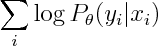
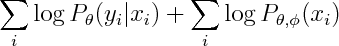
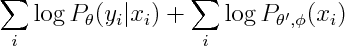
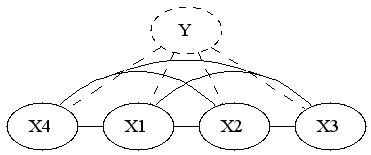
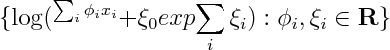
 If you've used cell phones to send text messages you probably know about their auto-complete feature. For those that haven't -- each digit corresponds to 3 or 4 letters, you enter the digits consistent with your word, and it tries to guess which word you meant. For instance you enter "43556", and it will automatically guess "hello". But if you enter "785" to mean "SVM", it'll probably guess "run", and you'll have to back-up and re-enter the word. The challenge is for the phone to guess the right word.
If you've used cell phones to send text messages you probably know about their auto-complete feature. For those that haven't -- each digit corresponds to 3 or 4 letters, you enter the digits consistent with your word, and it tries to guess which word you meant. For instance you enter "43556", and it will automatically guess "hello". But if you enter "785" to mean "SVM", it'll probably guess "run", and you'll have to back-up and re-enter the word. The challenge is for the phone to guess the right word.