Neural Networks making a come-back?

Five years ago I ran some queries on Google Scholar to see trends on the number of papers that mention particular phrase. The number of hits for each year was divided by the number of hits for "machine learning". Back then it looked like NN's started gaining in popularity with invention of back-propagation in 1980's, peaked in 1993 and went downhill from there.



Since then, there's been several major NN developments, involving deep learning and probabilistically founded versions so I decided to update the trend. I couldn't find a copy of scholar scraper script anymore, luckily Konstantin Tretjakov has maintained a working version and reran the query for me.



It looks like downward trend in 2000's was misleading because not all papers from that period have made it into index yet, and the actual recent trend is exponential growth!

One example of this "third wave" of Neural Network research is unsupervised feature learning. Here's what you get if you train a sparse auto-encoder on some natural scene images



What you get is pretty much a set of Gabor filters, but the cool thing is that you get them from your neural network rather than image processing expert

Another ML blog

I just noticed that Justin Domke has a blog --

He's one of the strongest researchers in the field of graphical models. I first came across his dissertation when looking for a way to improve loopy-Belief Propagation based training. His thesis gives one such idea -- instead of maximizing the fit of an intractable model, and using BP as intermediate step, maximize the fit of BP marginals directly. This makes sense since approximate (BP-based) marginals are what you ultimately use.

If you run BP for k steps, then likelihood of the BP-approximated model is tractable to minimize -- calculation of gradient is very similar to k steps of loopy BP. I derived formulas for gradient of "BP-approximated likelihood" in equations 17-21 in this note. It looks a bit complicated in my notation, but derivation is basically an application of chain rule to BP-marginal, which is a composition of k-steps of BP update formula.

Going to Google

I've accepted an offer from Google and will be joining their Tesseract team next week.

I first got interested in OCR when I faced a project at my previous job involving OCR of outdoor scenes and found it to be a very complex task, yet highly rewarding because it's easy to make incremental progress and see your learners working.

Current state-of-the-art OCR tools are not at human level of reading, partially because humans are able to take context into account. For instance, sentence below is unreadable if you don't assume English language.


Also, I'm excited to work on an open-source project. I'd like to live in a world where the best technologies are open-source and free to everyone.

Linear Programming for Maximum Independent Set

Maximum independent set, or "maximum stable" set is one of classical NP-complete problems described in Richard Karp's 1972 paper "Reducibility Among Combinatorial Problems". Other NP-complete problems often have a simple reduction to it, for instance, p.3 of Tony Jebara's "MAP Estimation, Message Passing, and Perfect Graphs" shows how MAP inference in an arbitrary MRF reduces to Maximum Weight Independent Set.

The problem asks to find the largest set of vertices in a graph, such that no two vertices are adjacent.



Finding largest independent set is equivalent to finding largest clique in graph's complement



A classical approach to solving this kind of problem is based on linear relaxation.

Take a variable for every vertex of the graph, let it be 1 if vertex is occupied and 0 if it is not occupied. We encode independence constraint by requiring that adjacent variables add up to 1. So we can consider the following graph and corresponding integer programming formulation:



$$\max x_1 + x_2 + x_3 + x_4 $$

such that
$$
\begin{array}{c}
x_1+x_2 \le 1 \\\\
x_2+x_3 \le 1 \\\\
x_3+x_4 \le 1 \\\\
x_4+x_1 \le 1 \\\\
x_i\ge 0 \ \ \forall i \\\\
x_i \in \text{Integers}\ \forall i
\end{array}
$$

Solving this integer linear integer program is equivalent to the original problem of maximum independent set, with 1 value indicating that node is in the set. To get a tractable LP programme we drop the last constraint.

If we solve LP without integer constraints and get integer valued result, the result is guaranteed to be correct. In this case we say that LP is tight, or LP is integral.

Curiously, solution of this kind of LP is guaranteed to take only values 0,1 and $\frac{1}{2}$. This is known as "half-integrality". Integer valued variables are guaranteed to be correct, and we need to use some other method to determine assignments to half-integer variables.

For instance below is a graph for which first three variables get 1/2 in the solution of the LP, while the rest of the vertices get integral values which are guaranteed to be correct



Here's what this LP approach gives us for a sampling of graphs



A natural question to ask is when this approach works. Its guaranteed to work for bipartite graphs, but it also seems to work for many non-bipartite graphs. None of the graphs above are bipartite.

Since independent set only allows one vertex per clique, we can improve our LP by saying that sum of variables over each clique has to below 1.

Consider the following graph that our original LP has a problem with:



Instead of having edge constraints, we formulate our LP with clique constraints as follows:

$$x_1+x_2+x_3\le 1$$
$$x_3+x_4+x_5\le 1$$

With these constraints, LP solver is able to find the integral solution



In this formulation, solution of LP is no longer half-integral. For the graph below we get a mixture of 1/3 and 2/3 in the solution.



Optimum of this LP is known as the "fractional chromatic number" and it is an upper bound both on the largest clique size and the largest independent set size. For the graph above, largest clique and independent set have sizes 9/3 and 12/3, whereas fractional chromatic number is 14/3.

This relaxation is tighter than previous, here are some graphs that previous LP relaxation had a problem with.



This LP is guaranteed to work for perfect graphs which is a larger class of graphs than bipartite graphs. Out of 853 connected graphs over 7 vertices, 44 are bipartite while 724 are perfect.

You can improve this LP further by adding more constraints. A form of LP constraints that generalizes previous two approaches is

$$\sum_{i\in C} x_i\le \alpha(C)$$

Where $C$ is some subgraph and $\alpha(C)$ is its independence number.

You extend previous relaxation by considering subgraphs other than cliques.
Lovasz describes the following constraint classes (p.13 of "Semidefinite programs and combinatorial optimization")

1. Odd hole constraints
2. Odd anti-hole constraints
3. Alpha-critical graph constraints.

Note that adding constraints for all maximal cliques can produce a LP with exponential number of constraints.

Notebook
Packages

Perils of floating point arithmetic

A recent discussion on stackoverflow brought up the issue of results of floating point arithmetic being non-reproducible

A reader asked what one could do to guarantee that result of floating point computation is always the same, and Daniel Lichtblau, a veteran developer at the kernel group of WRI replied that "it is impossible with current hardware and software"

One problem is that IEEE 754 standard is ambiguous, and different implementations of it give slightly different results. See page 250 of What Every Computer Scientist Should Know About Floating Point Arithmetic for specific examples. This means that compiling code on a different system can produce slightly different results.

Another issue is that even when you run the same computation on the same system, results can be slightly different on reruns. This has to do with how low-level optimization is scheduled.

This means that if you want your results to be reproducible, you should avoid things like testing floating point numbers for equality. John D Cook gives some more advice in Five Tips for Floating Point Programming

How to patent an algorithm in the US

Today I got Google Alert today on the following pending patent -- Belief Propagation for Generalized Matching. I like to stay up on Belief Propagation literature, so I took a closer look. The PDF linked gives a fairly detailed explanation of belief propagation for solving matching problems, including pseudocode which is very detailed, looking like an excerpt of a C program. Appendix A seems to be an expanded version of a paper which appeared in NIPS 2008 workshop

A pecularity of the US patent system is that patents on algorithms are not allowed, yet algorithms are frequently patented. A few years ago when I blogged on the issue of patents in Machine Learning, I didn't know the specifics, but now, having gone through the process, I know a bit more.

When filing an algorithm patent, patent lawyer will tell you to remove every instance of the word "algorithm" and replace it with some other word. This seems to be necessary for getting the patent through.

So, in the patent above, belief propagation algorithm is referred to as "belief propagation system". In the whole application, word "system" occurs 114 times, whereas "algorithm" occurs 1 time, in reference to a competing approach.

Another thing the patent lawyer will probably ask for is lots and lots of diagrams. I'm guessing that diagrams serve as further evidence that your algorithm is a "system" and not merely an algorithm. There are only so many useful diagrams you can have, so at some point you may find yourself pulling diagrams from thin ar and thinking "why am I doing this?" (but then remembering that it's because of the bonus). In the industry, a common figure seems to be $5000 for a patent that goes through. If a company doesn't have bonus structure, they may use other means to pressure employees into patent process. (note, patent above was filed through a university)

As a result, these kinds of patents end up with vacuous diagrams.

For instance, In the patent above, there are 17 figures, and a few of them don't seem to convey any useful information. The one below is illustrating the "plurality of belief propagation processors connected to a bus"


And this one is one is to illustrate belief propagation processors connected to a network


Finally when I saw the following diagram, I first thought it was there to illustrate BP update formula, which involves adding and multiplying numbers



But it's not even tenuously connected to the rest of the patent. 604 is supposed to be "computer readable media", 606 is a "link that couples media to the network", 608 is the "network" for aforementioned "link" and "media". 616 and 618 are not referenced.

This doesn't actually matter because nobody really reads the patent anyway. The most important part of getting the patent through is having a patent lawyer on the case who can frame it in the right format and handle communication with the patent office. The process for regular (non-expedited) patents can take five years and the total cost can exceed $50,000.

As to why an organization would spend so much time and money on a patent that might not even be enforceable by virtue of being an algorithm patent -- patents have intrinsic value. Once patent clears the patent office, a patent is an asset which can be sold or traded and as a result increases company worth. You can sell rights to pending patents before they are granted which makes the actual content of the patent even less important

Generalized Distributive Law

With regular distributive law you can do things like

$$\sum_{x_1,x_2,x_3} \exp(x_1 + x_2 + x_3)=\sum_{x_1} \exp x_1 \sum_{x_2} \exp x_2 \sum_{x_3} \exp x_3$$

This breaks the original large sum into 3 small sums which can be computed independently.

A more realistic scenario requires factorization into overlapping parts. For instance take the following

$$\sum_{x1,x2,x3,x_4,x_5} \exp(x_1 x_2 + x_2 x_3 + x_3 x_4+x_4 x_5)$$

You can't use directly apply distributive law here. Naive evaluation of the sum is exponential in the number of variables, however this problem can be solved in time linear in the number of variables.

Consider the following factorization
$$\sum_{x1,x2} \exp x_1 x_2 \left( \sum_{x_3} \exp x_2 x_3 \left( \sum_{x_4} \exp x_3 x_4 \left( \sum_{x_5} \exp x_4 x_5 \right) \right) \right) $$

Now note that when computing inner sums, naive approach results in same sum being recomputed many times. Save those shared pieces and you get an algorithm that's quadratic in number of variable values and linear in number of variables

Viterbi and Forward-Backward are specific names of this kind of dynamic programming for chain structured sums as above.

To consider tree-structured sum, take a problem of counting independent sets in a tree-structured graph. In this case we can use the following factorization




This is the first step of the recursion and you can repeat it until your pieces have tractable size.

Now for a general case of non-tree-structured graph, consider the sum below

$$\sum_{x1,x2,x3,x_4,x_5} \exp( x_1 x_2 + x_2 x_3 + x_3 x_4+x_4 x_5 + x_5 x_1 )$$

Here, variables form a loop, so regular tree recursion like Viterbi does not apply. However, this sum can be found efficiently, linear in the number of variables, and cubically in the number of variable values. I have more in depth explanation of decomposing problems like above in an answer on cstheory site but the basic idea is similar to the approach with independent sets -- fix some variables and recurse on subparts.

This kind of general factorization has been re-invented many times and is known as Generalized Distributive Law, tree-decomposition, junction tree, clique tree, partial k-tree, and probably a few other names.


Notebook

Cluster decomposition and variational counting

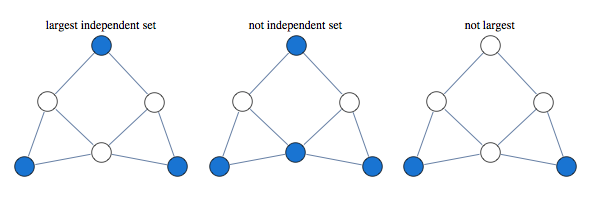
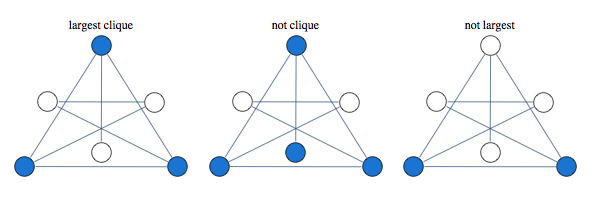
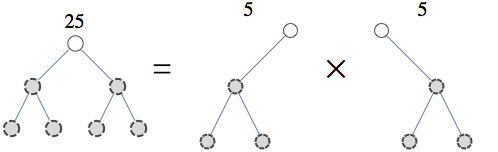
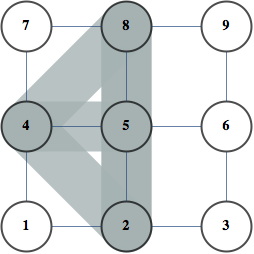
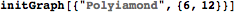Suppose we want to count the number of independent sets in a graph below.



There are 9 independent sets.


Because the graphs are disjoint we could simplify the task by counting graphs in each connected component separately and multiplying the result



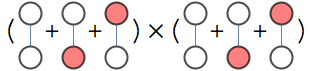
Variational approach is one way of extending this decomposition idea to connected graphs.

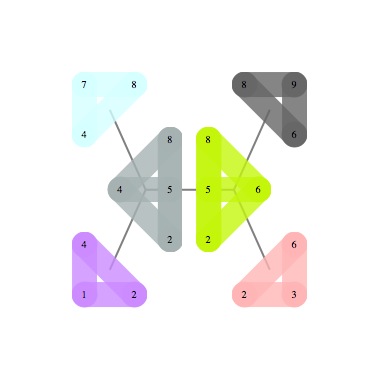
Consider the problem of counting independent sets in the following graph.


There are 7 independent sets. Let $x_i=1$ indicate that node $i$ is occupied, and $P(x_1,x_2,x_3,x_4)$ be a uniform distribution over independent sets, meaning it is either 1/7 or 0 depending whether $x_1,x_2,x_3,x_4$ forms an independent set

Entropy of uniform distribution over $n$ independent sets distribution is $H=-\log(1/n)$, hence $n=\exp H$, so to find the number of independent sets just find the entropy of distribution $P$ and exponentiate it.

We can represent P as follows

$$P(x_1,x_2,x_3,x_4)=\frac{P_a(x_1,x_2,x_3)P_b(x_1,x_3,x_4)}{P_c(x_1,x_3)}$$

Entropy of P similarly factorizes

$$H=H_a + H_b - H_c$$

Once you have $P_A$, $P_B$ and $P_C$ representing our local distributions of our factorization, we can forget the original graph and compute the number of independent sets from entropies of these factors

To find factorization of $P$ into $P_a,P_b$, and $P_c$ minimize the following objective

$$KL(\frac{P_a P_b}{P_c},P)$$

This is KL-divergence between our factorized representation and original representation. Message passing schemes like cluster belief propagation can be derived as one approach of solving this minimization problem. In this case, cluster belief propagation takes 2 iterations to find the minimum of this objective. Note that the particular form of distance is important. We could reverse the order and instead minimize $KL(P,P_a P_b/P_c)$ and while this makes sense from approximation stand-point, minimizing reversed form of KL-divergence is generally intractable.


This decomposition is sufficiently rich that we can model P exactly using proper choice of $P_a,P_b$ and $P_c$, so the minimum of our objective is 0, and our entropy decomposition is exact.

Now, the number of independent sets using decomposition above factorizes as
$$n=\exp H=\frac{\exp H_a \exp H_b}{\exp H_c} = \frac{\left(\frac{7}{2^{4/7}}\right)^2}{\frac{7}{2\ 2^{1/7}}} = \frac{4.75 \times 4.75}{3.17}=7$$

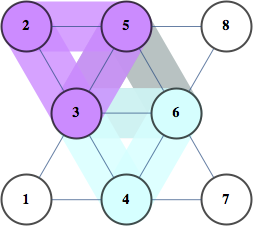
Our decomposition can be schematically represented as the following cluster graph



We have two regions and we can think of our decomposition as counting number of independent sets in each region, then dividing by number of independent sets in the vertex set shared by pair of connected regions. Note that region A gets "4.75 independent sets" so this is not as intuitive as decomposition into connected components


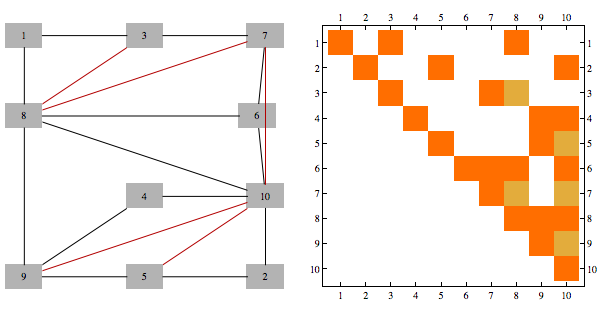
Here's another example of graph and its decomposition.





Using 123 to refer to $P(x_1,x_2,x_3)$ the formula representing this decomposition is as follows

$$\frac{124\times 236\times 2456 \times 4568 \times 478\times 489}{24\times 26 \times 456 \times 48 \times 68}$$

There are 63 independent sets in this graph, and using decomposition above the count decomposes as follows:

$$63=\frac{\left(\frac{21\ 3^{5/7}}{2\ 2^{19/21} 5^{25/63}}\right)^2 \left(\frac{3\ 21^{1/3}}{2^{16/21} 5^{5/63}}\right)^4}{\frac{21\ 3^{3/7}}{2\ 2^{1/7} 5^{50/63}} \left(\frac{3\ 21^{1/3}}{2\ 2^{3/7} 5^{5/63}}\right)^4}$$


Finding efficient decomposition that models distribution exactly requires that graph has small tree-width. This is not the case for many graphs, such as large square grids, but we can apply the same procedure to get cheap inexact decomposition.

Consider the following inexact decomposition of our 3x3 grid



Corresponding decomposition has 4 clusters and 4 separators, and the following factorization formula

$$\frac{1245\times 2356 \times 4578 \times 5689}{25\times 45 \times 56 \times 58}$$

We can use minimization objective as before to find the parameters of this factorization. Since original distribution can not be exactly represented in this factorization, result will be approximate, unlike previous two example.

Using message-passing to solve the variational problem takes about 20 iterations to converge, to an estimate of 46.97 independent sets




To try various decompositions yourself, unzip the archive and look at usage examples in indBethe3-test.nb

Notebooks

Junction trees in numerical analysis

There's a neat connection between Cholesky factorization and graph triangulations -- graph corresponding to Cholesky factorization of a sparse matrix is precisely the triangulation of the sparse matrix (when viewed as a graph) using canonical elimination ordering.

Here's an example of a matrix (corresponding to the graph with black edges only), and its Cholesky factorization. We triangulate the graph by any pairs of neighbors of v which have higher index than v, for every v. Extra edges added in this way correspond to extra non-zero entries in Cholesky decomposition of the original matrix. Different color edges/matrix entries correspond to non-zero entries in Cholesky factorization not present in original matrix



Furthermore, junction tree we get using min-fill heuristic of a graph is same structure as what is used to perform Cholesky factorization using parallel multi-frontal method

Here's a chordal matrix in perfect order and its Cholesky factorization


The fact that Cholesky factorization has the same sparsity structure as the original matrix confirms that its a chordal matrix in perfect elimination order

Here's the graph representation of the matrix


Junction tree decomposition of this graph reveals the following clique structure


High branching structure of decomposition means that Cholesky factorization can be highly parallelized, in particular, the very last step of Cholesky decomposition of this matrix in minfill order consists of 32 independent tasks that can be done in parallel.

I packaged together some Mathematica code for these kinds of tasks

Building Junction Trees

Here's a 367 vertex Apollonian Network and its Junction Tree (aka Tree Decomposition)





A Junction Tree provides an efficient data structure to do exact probabilistic inference. In the context of traditional graph algorithms, it is known as the "Tree Decomposition". The amount of structure apparent from the junction tree shows that problems structured as Apollonian Networks have very low computational complexity.

The same junction tree structure can also be used to efficiently compute chromatic polynomials, find cliques, count self-avoiding walks, and the reason for this universality is that it essentially captures separation structure of the graph -- it is a representation of a complete set of vertex separators. In the Junction Tree above you can see 121 non-leaf nodes that separate the graph into 3 parts. Each node corresponds to a set of 4 vertices. There are also 363 edges, each corresponds to a set of 3 vertices that separates the graph into 2 parts. The fact that the graph can be recursively partitioned using small separators implies an efficient recursion scheme for problems on this graph.

I put together a Mathematica package to build Junction Trees like above using MinFill, MinCut and a few other heuristics. Some experimenting showed MinFill with Vertex Eccentricity for choosing between vertices with equal fill to work the best for general graphs, whereas MinCut worked the best for planar graphs.

P vs. NP page

Here's a page linking 65 attempts of resolving P vs NP problem. A couple of papers were published in peer-reviewed journals or conferences, while most are "arxiv" published. Some statistics:

• 35 prove P=NP
  
• 28 prove P!=NP
  
• 2 prove it can go either way (undecidable)
  

towards Problem Compilers

First programmers wrote in machine code and assemblers simplified this task significantly by letting them give algorithms at a higher level. I still find stacks of punch cards like below in my St.Petersburg home



Wouldn't it be great if we could extend this idea further and have the computer compile the problem into machine code?

Actually, we already have such tools restricted to various versions of "problem language". For instance if you express your problem in terms of integer optimization, you can use integer programming tools.

Another language is the language of "graphical models". In the most general formulation, you specify meaning of operations + and *, that obey distributive law, set of x variables, set of functions f, and ask computer to find the following

$$\bigoplus_{x_1,x_2,\ldots} \bigotimes_f f(x)$$

This formulation has a natural "interactions graph" associated with it, and a computer can find an algorithm to solve this problem using tree decomposition if interactions between f functions are not too complex

However, this is still suboptimal because the algorithm designer needs to pick variables x and functions f, and this choice is fairly important. For instance, for minimum weight Steiner Tree, "natural" variables of the problem don't give a good factorization, and you need a smart designer to figure out a good reparameterization of the problem, like here.

As it stands right now, if a designer gives a good parameterization of the problem, a computer can solve it. Can we train a computer to find a parameterization?

I don't know the answer, but one potential approach to finding parameterizations is described in A new look at Generalized Distributive Law. They formulate the problem of optimal decomposition as that of search at the level of individual instantiations of x, so theoretically, this approach can discover optimal parameterization of the problem.

Interactive Tree Decomposition

Here's a tool (in Mathematica) to help visualize the process of constructing a Junction Tree. wrong link fixed

Clicking on vertices corresponds to vertex elimination and each click creates a new bag. After all vertices are eliminated, junction tree is created by removing redundant bags and taking the maximum spanning tree with size of the separators defining the weight of each edge as the junction tree.

If you try it on small examples, you can get some intuition of how outperform the greedy approach -- basically you want to find small separators of the graph, and at the same time you want those separators to have a lot of vertices in common

Happy New Year

Here are some links to start the new year on a light note

• Hinged tesselation
  
  
  
  
  
• Statistics-related Cartoons on stats.SE
  
  
  
  
  
  
  
• Memorable math paper titles, like Coxeter's "My Graph" (about Coxeter graph).
  
  
  
  
• Memorable Computer Science paper titles. It includes a series of papers "Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire", and "Seee More through Lenses than Bananas.". Apparently these are functional programming terms
  
  
  
  
  
• Annals of Improbable Research
  
  
  
  

Visualizing 7 dimensional simplex

Suppose we'd like to visualize a set of joint probabilities realizable by distributions of 3 binary variables.

It is a 7 dimensional regular simplex, and we could draw a lower dimensional section of it. There's an infinite number of sections, but there aren't that many *interesting* ones.

As an example, suppose we want to find a good 2 dimensional section of a 3 dimensional regular simplex. It seems reasonable to restrict attention to sections that go through simplex center and two other points, each of which is a vertex or a center of some edge or face. There are just 2 such sections determined up to rotation/reflection


For 7 dimensional simplex, we could similarly take 3 dimensional sections determined by simplex center and 3 points, each a centroid of some set of vertices. This gives 49 distinct shapes, shown below.


Among those, there's just one section that intersects all 8 faces of the simplex and preserves the underlying symmetry



Also known as the regular octahedron.

Implementation details

Computationally nice structures

One approach to solving hard problems is to break them into computationally efficient parts.

For instance, Globerson/Jaakkola do approximate counting by decomposing graph into planar graphs. In each part, the problem reduces to perfect matchings which can be solved efficiently on planar graph. Bouchet/Jordan decompose counting bipartite perfect matchings into much easier problems that count matchings perfect on "one side" of the graph. Sontag/Jaakola solve subproblems on star-shaped subgraphs of original graph, the symmetry of star graph enabling a very fast solution to each subproblem.

I recently came across graph class database which gives information on thousands of graph classes. It shows dozens (hundreds?) distinct tractable classes for exact maximum independent set, and most of them seem to have unbounded tree width. I haven't heard of most of those classes and would be curious to know how many distinctly interesting algorithms they correspond to

Here are a few computationally nice structures I've seen employed in Machine Learning and Vision literature

Upper-bounded tree width

Everything is easy via tree decomposition

Lower-bounded girth

Almost everything is easy via loopy belief propagation

Planar

Easy minimization of submodular functions. Easy counting of certain structures by reduction to perfect matchings.

Complete

Easy counting of unweighted local structures

Perfect

Easy MAP inference with NAND potentials

Star

Very efficient updates for MAP inference

Claw-free

A generalization of line graphs. Easy maximum independent set, and counting by reduction to matchings


Any other useful classes I missed?
Mathematica notebook