It is a 7 dimensional regular simplex, and we could draw a lower dimensional section of it. There's an infinite number of sections, but there aren't that many *interesting* ones.
As an example, suppose we want to find a good 2 dimensional section of a 3 dimensional regular simplex. It seems reasonable to restrict attention to sections that go through simplex center and two other points, each of which is a vertex or a center of some edge or face. There are just 2 such sections determined up to rotation/reflection
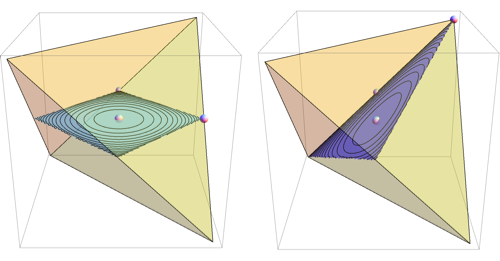
For 7 dimensional simplex, we could similarly take 3 dimensional sections determined by simplex center and 3 points, each a centroid of some set of vertices. This gives 49 distinct shapes, shown below.

Among those, there's just one section that intersects all 8 faces of the simplex and preserves the underlying symmetry

Also known as the regular octahedron.
Implementation details
THANKS FOR THE INFORMATION...
ReplyDelete<a href="http://www.chloros.in/digital-marketing-internship.htmlhttp://www.chloros.in/digital-marketing-internship.html>Digital Marketing Internship Program in Bangalore</a>
ReplyDeleteExcellent machine learning blog,thanks for sharing...
Seo Internship in Bangalore
Smo Internship in Bangalore
Digital Marketing Internship Program in Bangalore
I wonder if we may share this with Alan Wallace and Lama Padma Samten
ReplyDeleteThanks for the information... I really love your blog posts..
ReplyDeletehow to learn matlab |computer science summer internships |iot online courses |number 1 summer and winter internship training and workshop service provider in india. |online c programming classes
|machine learning training | data science course fees in coimbatore |internship opportunities for engineering students |electronic engineering summer internships |wordpress training in chennai
Eine Handvoll Websites, die sich im Folgenden als umfassend erweisen, sind aus unserer Sicht zweifellos einen Besuch wert.
ReplyDeleteThank you for the very useful information.
ReplyDelete프리미어카지노 도메인 주소 KRWIN
ReplyDeleteIn love with this post, thankyou for the information.
This is very nice one and gives indepth information. Please take a look at my website as well
ReplyDeleteThanks for providing a one-stop destination for useful information
ReplyDeleteThese are in fact impressive ideas in on the topic of blogging.
ReplyDeleteYou have touched some nice things here.