non-asymptotic uses of Central Limit Theorem

Suppose we throw a fair coin n times and estimate it's bias by averaging the number of heads observed. What is the squared error of this estimator?

Using standard binomial identities we can calculate this quantity exactly

$$\sum_{k=0}^n {n\choose k} 2^{-n} (\frac{k}{n}-\frac{1}{2})^2=\frac{1}{4n}$$

Another approach is to use the Central Limit Theorem to approximate exact density with a Gaussian. Using differentiation trick to evaluate the Gaussian integral we get the following estimate of the error

$$\int_{-\infty}^\infty \sqrt{\frac{2}{\pi n}} \exp(-2n(\frac{k}{n}-\frac{1}{2})^2)(\frac{k}{n}-\frac{1}{2})^2 dk=\frac{1}{4n}$$

You can see that using "large-n" approximation in place of exact density gives us the exact result for the error! This hints that Central Limit Theorem could be good for more than just asymptotics.

To see why this approximation gives exact result, rearrange the densities above to get an approximate value of k'th binomial coefficient

$${n\choose k} \approx \sqrt{\frac{2}{\pi n}} \exp(-2n(\frac{k}{n}-\frac{1}{2})^2) 2^n$$

Below are exact and approximate binomial coefficients for n=10, you can see it's fairly close


This is similar to an approximation we'd get if we used Stirling's approximation. However, Stirling's approximation always overestimates the coefficient, whereas error of this approximation is more evenly distributed. Here's plot of logarithm of error of our approximation and one using Stirling's, top curve is Stirling's approximation.


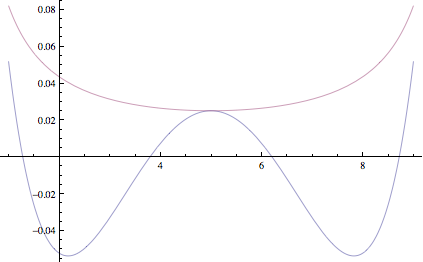
You can see that errors in the estimate due to CLT are sometimes negative and sometimes positive and in the variance calculation above, they happen to cancel out exactly